Polaris6G's blog

Stay humble,stay hungry.

0%

蓝桥杯-5

Posted on Valine:

学习回溯法与剪枝

回溯法

1.求子集问题

有一个含n个整数的数组a，所有元素均不相同，设计一个算法求其所有子集（幂集）。

思路：解空间为子集树。

使用x[]表示解向量：

  • 不选择a[i]元素->下一个状态为(x[i]=0, i+1)
  • 选择a[i]元素->下一个状态为(x[i]=1, i+1)

深搜+回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<bits/stdc++.h>
using namespace std;
#define MAXN 100

void dispasolution(int a[],int n,int x[])
{
	printf("(");
	for(int i=0;i<n;i++)
		if(x[i]==1)
			printf("%d",a[i]);
	printf(")");
	return;
}

void dfs(int a[],int n,int i,int x[]) 
{
	if(i>=n)
		dispasolution(a,n,x);
	else{
		x[i]=0;dfs(a,n,i+1,x); //不选择a[i] 
		x[i]=1;dfs(a,n,i+1,x); //选择a[i] 
	}
}

int main(){
	int a[]={1,2,3,4};
	int n = sizeof(a)/sizeof(a[0]);
	int x[MAXN];
	memset(x,0,sizeof(x));
	printf("求解结果\n");
	dfs(a,n,0,x);
	printf("\n");
	return 0;
}

2. 符号插入凑整

设计一个算法在1，2，…，9（顺序不能变）数字之间插入+或-或什么都

不插入，使得计算结果总是100的程序，并输出所有的可能性。

例如：1+2+34-5+67-8+9=100.

思路：

利用回溯法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<bits/stdc++.h>
using namespace std;
#define N 9

void fun(char op[],int sum,int pre,int a[],int i)
{
	if(i==N){
		if(sum==100){//打印 
			printf("%d",a[0]);
			for(int j=1;j<N;j++){
				if(op[j]!=' ')
					printf("%c",op[j]);
				printf("%d",a[j]);
			}
			printf("=100\n");
		}
		return;//递归出口 
	}
	
	op[i]='+';
	sum+=a[i];
	fun(op,sum,a[i],a,i+1);
	sum-=a[i];//回溯 
	
	op[i]='-';
	sum-=a[i];
	fun(op,sum,a[i],a,i+1);
	sum+=a[i];//回溯 
	
	op[i]=' ';
	sum-=pre;
	int tmp;
	tmp = pre*10 + a[i];
	sum+=tmp;
	fun(op,sum,tmp,a,i+1);
	sum-=tmp;
	sum+=pre;//回溯 
}

int main(){
	int a[N]={1,2,3,4,5,6,7,8,9};
	char op[N];
	fun(op,a[0],a[0],a,1);
	return 0;
}

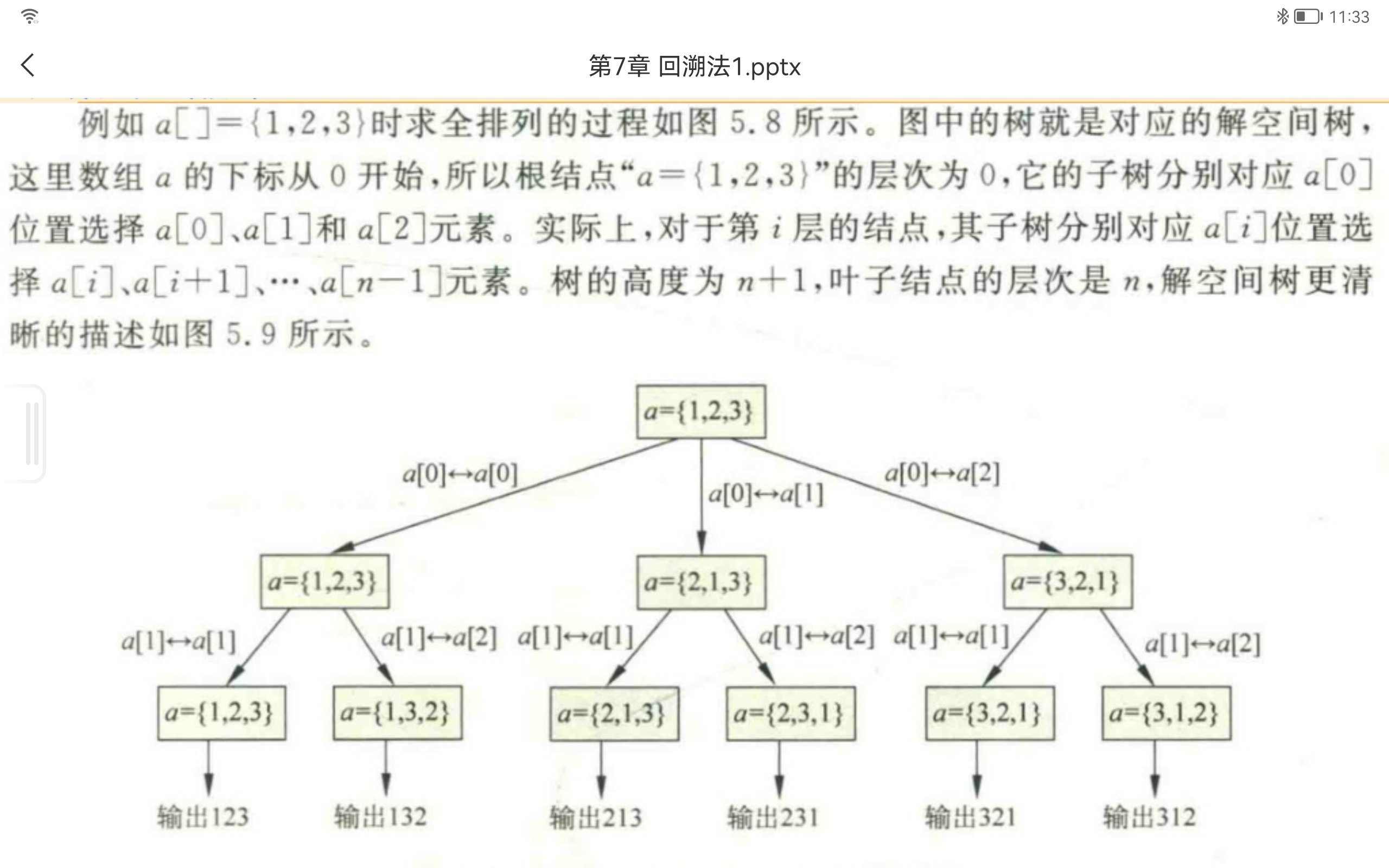
3.全排列问题

有一个含n个整数的数组a，所有元素均不相同，求其所有元素的全排列。例如，a[]={1,2,3}，得到结果是（1,2,3）、（1,3,2）、（2,3,1）、（2,3,1）

思路：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<bits/stdc++.h>
using namespace std;

void display(int a[],int n){
	printf("(");
	for(int i=0;i<n-1;i++)
		printf("%d,",a[i]);
	printf("%d)",a[n-1]);
	return;
}

void dfs(int a[],int n,int i){
	if(i>=n)display(a,n);
	else{
		for(int j=i;j<n;j++){
			swap(a[i],a[j]);
			dfs(a,n,i+1);
			swap(a[i],a[j]);//回溯恢复 
		}
	}
	return; 
}

int main(){
	int a[]={1,2,3};
	int n=sizeof(a)/sizeof(a[0]);
	dfs(a,n,0);
	printf("\n");
	return 0; 
}

回溯法与深搜的异同

相同点

  • 都遵循深度优先，即一步一步向前探索

不同点

  • 访问序不同：深度优先遍历目的是遍历，本质无序；回溯法目的是求解过程，本质有序
  • 访问次数不同：回溯法访问过的节点可能再次访问
  • 剪值的不同：回溯算法可采用剪枝条件剪除不必要的分枝以提高效能

0/1背包问题

有n个重量分别为{w1,w2,...wn}的物品，它们的价值分别为{v1,v2,…vn}，给定一个容量为W的背包。设计从这些物品中选取一部分物品放入该背包的方案，每个物品要么选中要么不选中，要求选中的物品不仅能够放在背包中，而且满足重量限制具有最大的价值。

思路：

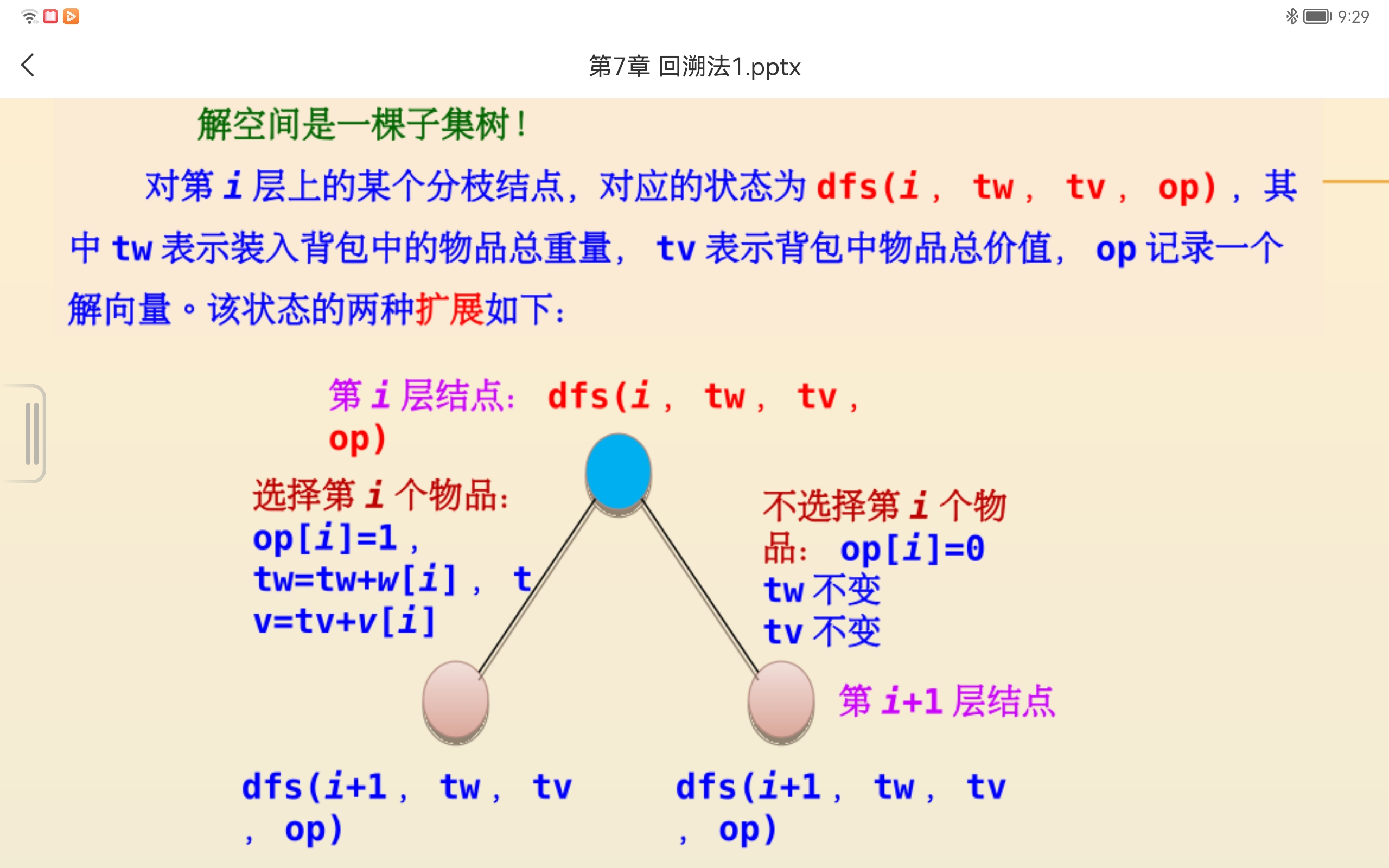
考虑装入背包中物品重量和恰好为W：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<bits/stdc++.h>
using namespace std;
#define MAXN 5
int n=4;//四件物品
int W=6;//书包最大总重量
int w[]={0,5,3,2,1};
int v[]={0,4,4,3,1};
int x[MAXN];//存放最终解 
int maxv;//存放最有解的总价值 
//int maxw;

void dfs(int i,int tw,int tv,int op[]){
	if(i>n){
		if(tw==W&&tv>maxv){
			maxv=tv;
			for(int j=1;j<=n;j++)
				x[j]=op[j];
		}
	}
	else{
		op[i]=1;
		dfs(i+1,tw+w[i],tv+v[i],op);
		
		op[i]=0;
		dfs(i+1,tw,tv,op);
	}
}

int main(){
	int op[5];
	dfs(1,0,0,op);
	cout<<maxv<<endl;
	for(int i=1;i<=n;i++)
	{
		if(i!=n)
		cout<<x[i]<<' ';
		else cout<<x[i]<<endl;	
	}	
	return 0;
}

改进1

左剪枝：

仅仅扩展满足tw+w[i]<=W的节点

改进2

右剪枝：

rw=w[i]+w[i+1]+...+w[n]

仅仅扩展满足tw+rw-w[i]>=W的节点 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void dfs(int i,int tw,int tv,int rw,int op[]){
	if(i>n){
		if(tw==W&&tv>maxv){
			maxv=tv;
			for(int j=1;j<=n;j++)
				x[j]=op[j];
		}
	}
	else{
        if(tw+w[i]<=W){//进行左剪枝
            op[i]=1;
			dfs(i+1,tw+w[i],tv+v[i],rw-w[i],op);
        }
		if(tw+rw-w[i]>=W)
        {
         	op[i]=0;
			dfs(i+1,tw,tv,rw-w[i],op);  
        }	
	}
}

考虑装入背包中物品重量和不超过W：

  • 左剪枝相同
  • 右剪枝修改：

上界函数bound(i)=tv+r表示沿着该方向选择得到物品的价值上界，r表示剩余物品的总价值。

若当前bound(i)<=maxv，则右剪枝，否则继续扩展。

显然r越小，bound(i)也越小，剪枝越多，为了构造更小的r，将所有物品以单位重量价值递减排列。

1
2
3
4
5
6
7
8
9
10
11
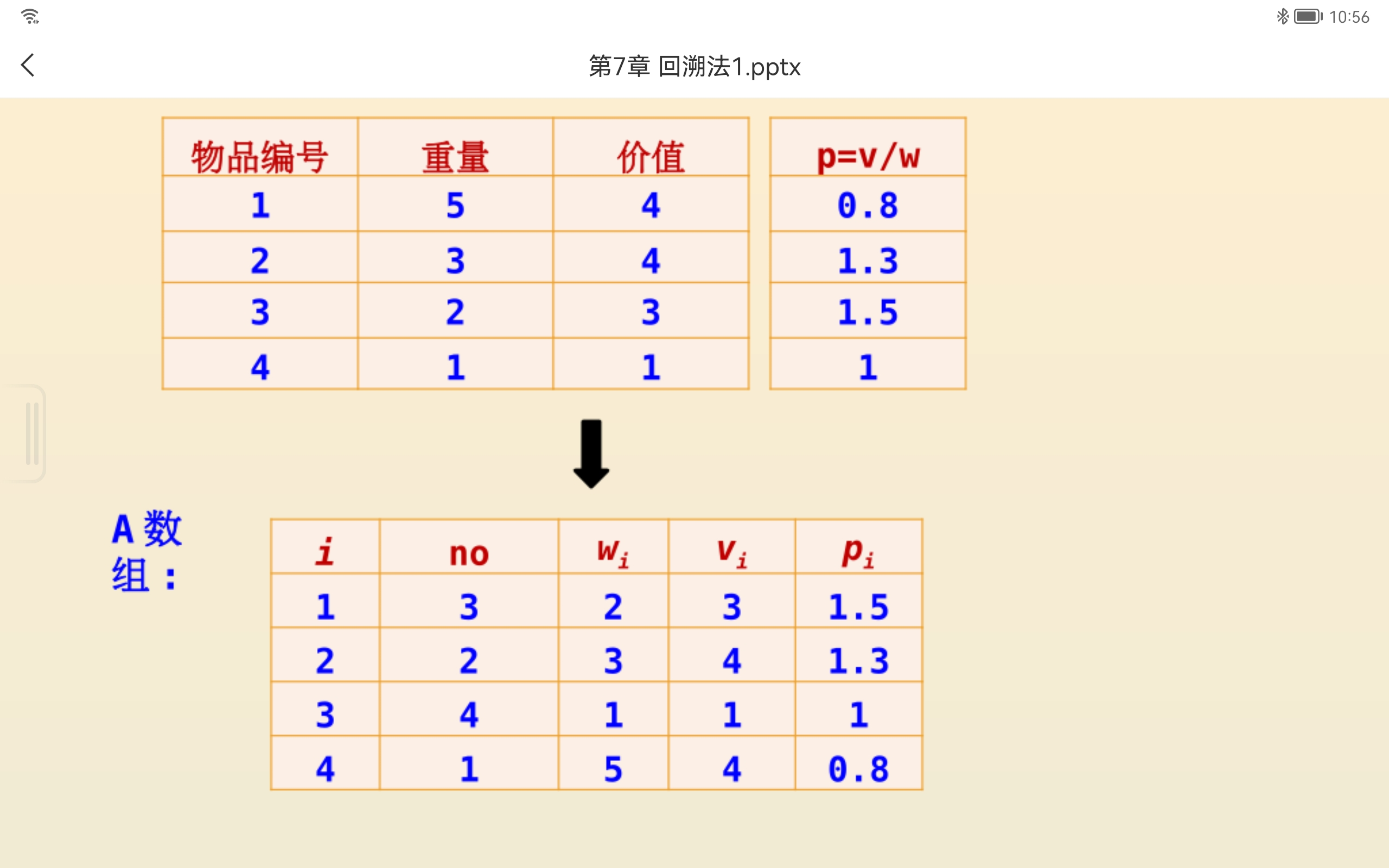
12
int bound(int i,int tw,int tv)//求上界
{
    i++;//从i+1开始
    while(i<=n && tw+A[i].w<=W){//若序号为i的物品可以整个放入
        tw+=A[i].w;
        tv+=A[i].v;
        i++;
    }
    if(i<=n)
        return tv+(W-tw)*A[i].p;//序号为i的物品不能整个放入
    else return tv;
}

右剪枝：仅仅扩展bound(i,tw,tv)>maxv的右孩子节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void dfs(int i,int tw,int tv,int rw,int op[]){
	if(i>n)
	{
		maxv=tv;
		for(int j=1;j<=n;j++)
			x[j]=op[j];
	}
	else{
        if(tw+A[i].w<=W){//进行左剪枝
            op[i]=1;
			dfs(i+1,tw+A[i].w,tv+A[i].v,op);
        }
		if(bound(i,tw,tv)>maxv)//进行右剪枝
        {
         	op[i]=0;
			dfs(i+1,tw,tv,op);  
        }	
	}
}

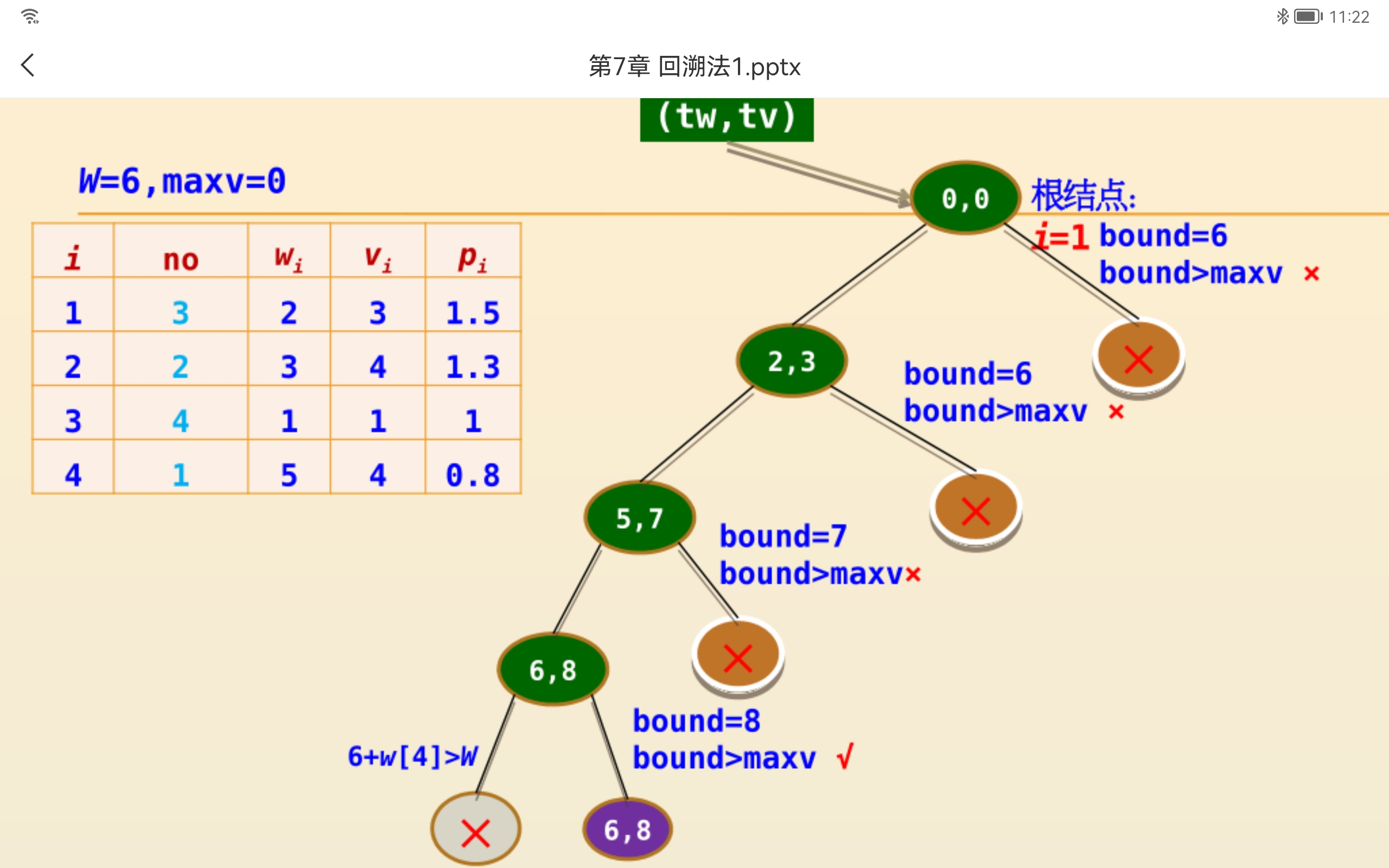
求解装载问题