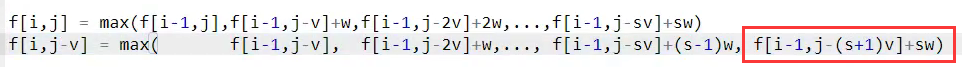Polaris6G's blog

Stay humble,stay hungry.

0%

算法基础05

Posted on Edited on Valine:

学习动态规划

常用模型

  • 背包
  • 线性DP
  • 计数类DP
  • 数位统计DP
  • 状态压缩DP
  • 树形DP
  • 记忆化搜索

闫式DP

没有模板，理解分析方式（集合的思想）

背包

模板问题：有n个物品和容量为v的背包，每件物品有体积vi和价值wi，问能装下的最大价值w

01背包

每件物品只能用1次（0,1）

Dp:

  • 状态表示f(i,j)

    • 集合

      • 表示所有选法
      • 条件：
        1. 只从前i个物品中选
        2. 总体积<=j

    • 属性：

      Max、Min、数量

  • 状态计算

    ->集合划分：f(i,j)

    -> 不含i情况f(i-1, j) + 含i情况f(i-1, j - vi) + wi

得到公式：dp[i][j] = Math.max(dp[i][j], dp[i-1][j-v[i]] + w[i]);

二维dp实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import java.io.*;

public class Main{
    static int N = 1010;
    static int n, m;
    static int[] v = new int[N];
    static int[] w = new int[N];
    static int[][] dp = new int[N][N];
    
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] str = br.readLine().split(" ");
        int n = Integer.parseInt(str[0]);
        int m = Integer.parseInt(str[1]);
        for(int i = 1; i <= n; i++){//注意下标
            String[] s = br.readLine().split(" ");
            v[i] = Integer.parseInt(s[0]);
            w[i] = Integer.parseInt(s[1]);
        }
        
        for(int i = 1; i <= n; i++){
            for(int j = 0; j <= m; j++){
                dp[i][j] = dp[i-1][j];
                if(j >= v[i]){
                    dp[i][j] = Math.max(dp[i][j], dp[i-1][j-v[i]] + w[i]);
                }
            }
        }
        System.out.println(dp[n][m]);
    }
}

dp优化：二维等价成一维

因为：i只用到了i-1，将i删去，交换循环方向

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import java.io.*;
//一维实现降低空间复杂度
public class Main{
    static int N = 1010;
    static int n, m;
    static int[] v = new int[N];
    static int[] w = new int[N];
    static int[] dp = new int[N];
    
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] str = br.readLine().split(" ");
        int n = Integer.parseInt(str[0]);
        int m = Integer.parseInt(str[1]);
        for(int i = 1; i <= n; i++){//注意下标
            String[] s = br.readLine().split(" ");
            v[i] = Integer.parseInt(s[0]);
            w[i] = Integer.parseInt(s[1]);
        }
        
        for(int i = 1; i <= n; i++){
            for(int j = m; j >= v[i]; j--){//巧妙改变顺序 保证计算的是dp[i-1][j-v[i]] 正序则dp[i][j-v[i]]会被提前计算
                dp[j] = Math.max(dp[j], dp[j-v[i]] + w[i]);
            }
        }
        System.out.println(dp[m]);
    }
}

完全背包

每件物品有无限个

Dp:

  • 状态表示f(i,j)

    • 集合

      • 表示所有选法
      • 条件：
        1. 只从前i个物品中选
        2. 总体积<=j

    • 属性：

      Max、Min、数量

  • 状态计算

    ->集合划分：f(i,j)

    -> 没有选i的情况f(i - 1, j) + 选了k个i的情况f(i - 1, j - k * vi) + k * w[i]（可合并）

三维实现：

1
2
3
4
5
for(int i = 1; i <= n; i++)
    for(int j = 0; j <= m; j++)
        	for(int k = 0; k * v[i] <= j; k++)
                f[i][j] = Math.max(f[i][j], f[i-1][j - k * v[i]] + k * w[i]);
System.out.println(f[n][m]);

dp优化：

得到公式：f(i, j) = Max(f[i - 1, j], f[i, j - v] + w)

可以理解为分为不含i的情况 + 至少含一次i的情况

1
2
3
4
5
6
for(int i = 1; i <= n; i++)
    for(int j = 0; j <= m; j++)
        f[i][j] = f[i-1][j];
        if(j >= v[i])
	        f[i][j] = Math.max(f[i][j], f[i][j - v[i]] + w[i]);
System.out.println(f[n][m]);

可以看出01背包问题是i - 1，完全背包问题是i

那么完全背包也可以优化成一维：

1
2
3
for(int i = 1; i <= n; i++)
	for(int j = v[i]; j <= m; j++)
		dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);

多重背包

限定每个物品有si个（有限）

Dp:

  • 状态表示f(i,j)

    • 集合

      • 表示所有选法
      • 条件：
        1. 只从前i个物品中选
        2. 总体积<=j

    • 属性：

      Max、Min、数量

  • 状态计算

    ->集合划分：f(i,j)

    -> 没有选i的情况f(i - 1, j) + 选了k个i的情况f(i - 1, j - k * vi) + k * w[i]（可合并）

朴素三位和完全背包类似：

复杂度: O(v w s)

1
2
3
4
5
for(int i = 1; i <= n; i++)
    for(int j = 0; j <= m; j++)
        	for(int k = 0; k <= s[i] && k * v[i] <= j; k++)
                f[i][j] = Math.max(f[i][j], f[i-1][j - k * v[i]] + k * w[i]);
System.out.println(f[n][m]);

然而多重背包问题不能用完全背包优化 ， 因为是多重背包不能确定是否有最后一项（因为s不一定可使背包边满），而完全背包一定每有最后一项。

二进制优化

将s[i]分组，以二进制为标准，分成1, 2, 4, 8, ..., 2^(k), c，其中c为s[i] - (2^(k+1) - 1)

可以证明，这组数可以表示0~s[i]之间的所有数

因为：1, 2, 4, 8, ..., 2^(k)可表示[0, 2^(k+1) - 1]中所有的数；加上c可表示[c, s[i]]中所有的数；而c <= 2 ^ (k+1)，两区间可以合并

这样对于每个s[i]，可以将其分为log(s[i])个数分别考虑选择，这样就可以将问题转换为n扩大到n * log(s[i])个数后进行01背包

复杂度：O(n m log[s])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import java.io.*;

public class Main{
    static int N = 11010;//1000 * Math.log(2, 2000)
    static int M = 2010;
    static int[] v = new int[N];
    static int[] w = new int[N];
    static int[] dp = new int[M];
    
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] str = br.readLine().split(" ");
        int n = Integer.parseInt(str[0]);
        int m = Integer.parseInt(str[1]);
        int cnt = 0;
        for(int i = 1; i <= n; i++){
            String[] arr = br.readLine().split(" ");
            int a = Integer.parseInt(arr[0]);
            int b = Integer.parseInt(arr[1]);
            int s = Integer.parseInt(arr[2]);
            int k = 1;
            while(k <= s){
                cnt++;
                v[cnt] = a * k;
                w[cnt] = b * k;
                s -= k;
                k *= 2;
            }
            if(s > 0){
                cnt++;
                v[cnt] = a * s;
                w[cnt] = b * s;
            }
        }
        n = cnt;//不要漏了
        for(int i = 1; i <= n; i++){//01背包
            for(int j = m; j >= v[i]; j--){
                dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
            }
        }
        System.out.println(dp[m]);
    }
}

分组背包问题

有n组物品，每组物品有若干个，但每组只能选一个物品

Dp:

  • 状态表示f(i,j)

    • 集合

      • 表示所有选法
      • 条件：
        1. 只从前i组物品中选
        2. 总体积<=j

    • 属性：

      Max、Min、数量

  • 状态计算

    ->集合划分：f(i,j)

    -> 第i组没有选的情况f(i - 1, j) + 第i组选了第k个的情况f(i - 1, j - v[i,k]) + w[i,k]

复杂度O(n^3)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import java.io.*;

public class Main{
    static int N = 110;
    static int[][] v = new int[N][N];
    static int[][] w = new int[N][N];
    static int[] s = new int[N];//第i组中物品数量
    static int[] dp = new int[N];
    
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] str = br.readLine().split(" ");
        int n = Integer.parseInt(str[0]);
        int m = Integer.parseInt(str[1]);
        for(int i = 1; i <= n; i++){
            s[i] = Integer.parseInt(br.readLine());
            for(int j = 1; j <= s[i]; j++){
                String[] arr = br.readLine().split(" ");
                v[i][j] = Integer.parseInt(arr[0]);
                w[i][j] = Integer.parseInt(arr[1]);
            }
        }
        for(int i = 1; i <= n; i++){
            for(int j = m; j >= 0; j--){
                for(int k = 1; k <= s[i]; k++){//注意这里遍历顺序不能变
                    if(j >= v[i][k])dp[j] = Math.max(dp[j], dp[j - v[i][k]] + w[i][k]);
                }
            }
        }
        System.out.println(dp[m]);
    }
}

线性DP

最长上升序列

给定一个长度为 N 的数列，求数值严格单调递增的子序列的长度最长是多少。

Dp:

  • 状态表示f(i)

    • 集合
      • 所有以i结尾的上升子序列
    • 属性：是Max

  • 状态计算

    ->集合划分：以该子序列倒数第二个数位置进行划分，分为i类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import java.util.Scanner;
import java.util.Arrays;

public class Main{
    static int N = 1010;
    static int[] a = new int[N];
    static int[] dp = new int[N];
    
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        for(int i = 1; i <= n; i++)a[i] = sc.nextInt();
        Arrays.fill(dp, 1);
        for(int i = 2; i <= n; i++){
            for(int j = 1; j < i; j++){
                if(a[i] > a[j])dp[i] = Math.max(dp[i], dp[j] + 1);
            }
        }
        int res = 0;
        for(int i = 1; i <= n; i++)res = Math.max(res, dp[i]);
        System.out.println(res);
    }
}

最长公共子序列

给定两个长度分别为 N 和 M 的字符串 A 和 B，求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。

Dp:

  • 状态表示f(i,j)

    • 集合
      • 所有在第一个序列的前i个字母中出现，且在第二个序列的前j个字母中出现的子序列
    • 属性：是Max

  • 状态计算

    ->集合划分：以a[i] b[j] 是否被选划分集合为4中情况

    00: dp[i-1, j-1]

    11: dp[i-1, j-1] + 1

    01: dp[i-1, j] 包含了a[i]不出现,b[j]出现的情况(01)

    10: dp[i, j-1] 包含了a[i]出现,b[j]不出现的情况(10)

    而01和10的情况中自然包含了00情况，于是代码中可以不写

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import java.util.Scanner;

public class Main{
    static int N = 1010;
    static int[][] f = new int[N][N];
    
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        String a = sc.next();
        String b = sc.next();
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= m; j++){
                f[i][j] = Math.max(f[i-1][j], f[i][j-1]);
                if(a.charAt(i-1) == b.charAt(j-1))f[i][j] = Math.max(f[i][j], f[i-1][j-1] + 1);
            }
        }
        System.out.println(f[n][m]);
    }
}

最短编辑距离

给定两个字符串 A 和 B，现在要将 A 经过若干操作变为 B，可进行的操作有：

删除–将字符串 A 中的某个字符删除。

插入–在字符串 A 的某个位置插入某个字符。

替换–将字符串 A 中的某个字符替换为另一个字符。

现在请你求出，将 A 变为 B 至少需要进行多少次操作。

Dp:

  • 状态表示f(i,j)

    • 集合
      • 所有将a[1~i]变成b[1~j]的操作方式
    • 属性：是Min

  • 状态计算：

    • 集合划分：根据最后一步操作

      删除a[i]：f[i-1][j] + 1

      插入a[i]：f[i][j-1] + 1

      替换a[i]：f[i-1][j-1] + 1

复杂度：O(3*n^2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import java.util.Arrays;
import java.util.Scanner;

public class Main {
	static int N = 1010;
	static int[][] f = new int[N][N];
	static int INF = (int)1e9;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		String a = sc.next();
		int m = sc.nextInt();
		String b = sc.next();
		//切记初始化
		for(int i = 0; i <= n; i++)f[i][0] = i;
		for(int j = 0; j <= m; j++)f[0][j] = j;
		
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				f[i][j] = Math.min(f[i - 1][j] + 1, f[i][j - 1] + 1);
				if (a.charAt(i - 1) == b.charAt(j - 1))
					f[i][j] = Math.min(f[i][j], f[i - 1][j - 1]);
				f[i][j] = Math.min(f[i][j], f[i - 1][j - 1] + 1);
			}
		}
		System.out.println(f[n][m]);
	}
}

区间DP

区间 DP 常用模版
所有的区间dp问题枚举时，第一维通常是枚举区间长度，并且一般 len = 1 时用来初始化，枚举从 len = 2 开始；第二维枚举起点 i （右端点 j 自动获得，j = i + len - 1）

模板代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
for (int len = 1; len <= n; len++) {         // 区间长度
    for (int i = 1; i + len - 1 <= n; i++) { // 枚举起点
        int j = i + len - 1;                 // 区间终点
        if (len == 1) {
            dp[i][j] = 初始值
            continue;
        }
        for (int k = i; k < j; k++) {        // 枚举分割点，构造状态转移方程
            dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + w[i][j]);
        }
    }
}

Dp:

  • 状态表示f(i,j)

    • 集合
      • 所有将第i堆石子到第j对石子合并成一堆石子的合并方式
    • 属性：是Min

  • 状态计算

    ->集合划分：以最后一步是左边哪一部分和右边哪一部分合并，即以分界线划分成j - i组 [i, k], [k + 1, j] k = [i, j-1]

    f[i][j] = min(f[i][k] + f[k+1][j] + s[j] - s[i-1])

复杂度：O(N^3)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import java.util.Scanner;

public class Main{
    static int N = 310;
    static int[] s = new int[N];
    static int[][] f = new int[N][N];
    static int INF = (int)2e9;
    
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        for(int i = 1; i <= n; i++){
            s[i] = sc.nextInt();
            s[i] += s[i - 1];
        }
        //len = 1时无需合并,f[i][i] = 0
        for(int len = 2; len <= n; len++){//先枚举长度 保证需要的f[][]提前被算好了
            for(int i = 1; i <= n - len + 1; i++){
                int l = i, r = i + len - 1;
                f[l][r] = INF;//求最小值切记要初始化
                for(int k = l; k < r; k++){
                    f[l][r] = Math.min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
                }
            }
        }
        System.out.println(f[1][n]);
    }
}

计数类DP

整数拆分

一个正整数 n 可以表示成若干个正整数之和，形如：n=n1+n2+…+nk，其中 n1≥n2≥…≥nk,k≥1。 我们将这样的一种表示称为正整数 n 的一种划分。 现在给定一个正整数 n，请你求出 n 共有多少种不同的划分方法。

方法一：理解为完全背包问题

Dp:

  • 状态表示f(i,j)

    • 集合
      • 选择1~i个数的和恰好为j的方案数
    • 属性：数量

  • 状态计算

    ->集合划分：以选择i的数量为划分依据，分为不选i，选s个i

    状态转移：f[i][j] = (f[i - 1][j] + sum(f[i - 1][j - s * i]))其中s * i <= j

    发现可以同完全背包问题一样得到优化如下：

    f[i][j] = (f[i - 1][j] + f[i][j - i])

    也可变成一维：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    import java.util.Scanner;

    public class Main{
        static int N = 1010;
        static int[] f = new int[N];
        static int mod = (int)1e9 + 7;
        
        public static void main(String[] args){
            Scanner sc = new Scanner(System.in);
            int n = sc.nextInt();
            f[0] = 1;
            for(int i = 1; i <= n; i++){
                for(int j = i; j <= n; j++){
                    f[j] = (f[j] + f[j - i]) % mod;
                }
            }
            System.out.println(f[n]);
        }
        
    }

方法二：

Dp:

  • 状态表示f(i,j)

    • 集合
      • 所有总和是i，并且恰好表示成j个正整数的和的方案数
    • 属性：数量

  • 状态计算

    ->集合划分：j个数的最小值是否为1

    为1，将1去掉得到f[i-1][j-1]；不为1，将所有数减1，得到f[i - j][j]

    状态转移：f[i][j] = f[i-1][j-1] + f[i - j][j]

    最终答案是res = sum(f[n][1~n])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import java.util.Scanner;

public class Main{
    static int N = 1010;
    static int[][] f = new int[N][N];
    static int mod = (int)1e9 + 7;
    
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        f[0][0] = 1;//注意初始化
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= i; j++){
                f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % mod;
            }
        }
        int res = 0;
        for(int i = 1; i <= n; i++)res = (res + f[n][i]) % mod;
        System.out.println(res);
    }
    
}

数位统计DP

计数问题：

给定两个整数 a 和 b，求 a 和 b 之间的所有数字中 0∼9 的出现次数。

0<a,b<100000000

求一个函数count(n ,x)表示1~n中x出现的次数(x = 0 ~ 9)

分情况讨论：

边界问题：

  • 当所求x出现在最高位时，没有(1)的情况
  • 当所求x = 0时，为了规避前导零的情况，abc != 0, 故是abc * 999
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
import java.util.Scanner;
import java.util.ArrayList;
import java.util.List;

public class Main{
    static int N = 10;
    
    static int get(List<Integer> list, int l, int r){
        int res = 0;
        for(int i = l; i >= r; i--){
            res = res * 10 + list.get(i);
        }
        return res;
    }
    
    static int power10(int x){
        int res = 1;
        while(x != 0){
            res *= 10;
            x--;
        }
        return res;
    }
    
    
    static int count(int n, int x){
        if(n == 0)return 0;
        List<Integer> l = new ArrayList<>();
        while(n != 0){
            l.add(n % 10);
            n /= 10;
        }
        int len = l.size();
        
        int res = 0;
        
        //0不需要枚举最高位
        for(int i = len - 1 - (x == 0 ? 1 : 0); i >= 0; i--){
            if(i < len - 1){
                res += get(l, len - 1, i + 1) * power10(i);
                if(x == 0)res -= power10(i);//前导零的情况
            }
            
            if(l.get(i) > x)res += power10(i);
            else if(l.get(i) == x) res += get(l, i - 1, 0) + 1;
        }
        return res;
    }
    
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        while(true){
            int a = sc.nextInt();
            int b = sc.nextInt();
            if(a == 0 && b == 0)break;
            if(a > b){
                int t = a;
                a = b;
                b = t;
            }
            for(int i = 0; i <= 9; i++){
                System.out.print(count(b, i) - count(a - 1, i) + " ");
            }
            System.out.println();
        }
    }
}

状态压缩DP

例题：

蒙德里安的梦想

求把 N×MN×M 的棋盘分割成若干个 1×2 的长方形，有多少种方案。

例如当 N=2，M=4 时，共有 5 种方案。当 N=2，M=3 时，共有 3 种方案。

如下图所示：

问给定N,M后的方案数。

1≤N,M≤11

解：

核心：先放横着的，再放竖着的

总方案数：只放横着的小方块的合法方案数

合法判断：所有剩余位置能否填充满竖着的小方块->可以按列来看。每一列内部所有连续的空着的小方块，需要是偶数个

Dp:

  • 状态表示f(i,j)

    • 集合
      • 已经将前i-1列摆好，且从第i-1列，伸出到第i列的状态是j（二进制）的所有方案
    • 属性：数量

  • 状态计算

    ->集合划分：根据i-1列伸出的小方格状态划分为2^n种情况

    条件：

    （1）(j&k) == 0(i-2列伸到i-1列的状态是k)

    （2）所有连续空着的位置的长度必须是偶数

    最终答案：f[m][0]第m+1列状态都为0的所有方案

时间复杂度：O(11 2^11 2^11)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
import java.io.*;
import java.util.*;

public class Main{
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static int N = 12, M = 1 << N;
    static long[][] f = new long[N][M];//动态规划数组
    static boolean[][] state = new boolean[M][M];//由一个状态i变到一个状态j是否合法
    static boolean[] st = new boolean[M];//表示0~2^n-1中的状态是否合法(偶数个0连续)
    
    
    public static void main(String[] args) throws IOException {
        while(true){
            String[] str = br.readLine().split(" ");
            int n = Integer.parseInt(str[0]);
            int m = Integer.parseInt(str[1]);
            if(n == 0 && m == 0)return;
            //预处理st数组
            for(int i = 0; i < 1 << n; i++){
                int cnt = 0;//表示当前前面0的个数
                boolean flag = true;
                for(int j = 0; j < n; j++){//枚举位数
                    if((i >> j & 1) == 1){
                        if(cnt % 2 == 1){
                            flag = false;//前面有奇数个0,不成立
                            break;
                        }
                        cnt = 0;//偶数个0恢复状态
                    }else cnt++;//如果当前不是1,cnt累加0的个数
                }
                //判断一下最后一层0的个数
                if(cnt % 2 == 1)flag = false;
                st[i] = flag;
            }
            //
            for(int i = 0; i < 1 << n; i++){
                Arrays.fill(state[i], false);//将状态清零防止上一组干扰
                for(int j = 0; j < 1 << n; j++){
                    //满足：1.i和j状态相同位不能同时为1
                    //2. 被i和j塞满的位置满足连续偶数个0
                    if((i & j) == 0 && st[i | j]){
                        state[i][j] = true;
                    }
                }
            }
            for(int i = 0; i < N; i++)Arrays.fill(f[i], 0);
            
            f[0][0] = 1;//初始化：空着也表示一种方案数
            for(int i = 1; i <= m; i++){//枚举每一列
               //枚举i - 1 到 i 的所有方案
               for(int j = 0; j < 1 << n; j++){
                   //枚举i - 2 到 i - 1的方案数
                   for(int k = 0; k < 1 << n; k++){
                       //现在的方案等于前面每种k方案的总和
                       if(state[j][k])f[i][j] += f[i - 1][k];
                   }
               }
            }
            System.out.println(f[m][0]);
        }
    }
}

最短Hamilton路径

给定一张 n 个点的带权无向图，点从 0∼n−1 标号，求起点 0 到终点 n−1 的最短 Hamilton 路径。 Hamilton 路径的定义是从 0 到 n−1 不重不漏地经过每个点恰好一次。

输出一个整数，表示最短 Hamilton 路径的长度。1≤n≤20 0≤a[i,j]≤107

Dp:

  • 状态表示f(i,j)

    • 集合
      • 所有从0走到j，走过的所有点状态是i（二进制 表示是否走过）的所有路径
    • 属性：Min

  • 状态计算

    ->集合划分：倒数第二个点是k （0,1,2,…,m）

    Min(f(i - {j}, k) )+ a(k, j)

复杂度：n * n * 2 ^ n

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import java.io.*;
import java.util.Arrays;

public class Main{
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static int N = 20;
    static int M = 1 << N;
    static int[][] w = new int[N][N];
    static int[][] f = new int[M][N];
    
    public static void main(String[] args) throws IOException {
        int n = Integer.parseInt(br.readLine());
        for(int i = 0; i < n; i++){
            String[] str = br.readLine().split(" ");
            for(int j = 0; j < n; j++){
                w[i][j] = Integer.parseInt(str[j]);
            }
        }
        
        for(int i = 0; i < 1 << n; i++){
            Arrays.fill(f[i], 0x3f3f3f3f);
        }
        
        f[1][0] = 0;//初始化0到0
        
        for(int i = 0; i < 1 << n; i++){
            for(int j = 0; j < n; j++){
                if((i >> j & 1) != 0){
                    for(int k = 0; k < n; k++){
                        if((i - (1 << j) >> k & 1) != 0)
                            f[i][j] = Math.min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
                    }
                }
            }
        }
        System.out.println(f[(1 << n) - 1][n-1]);
    }
}

树形DP

没有上司的舞会

Ural 大学有 N 名职员，编号为 1∼N。

他们的关系就像一棵以校长为根的树，父节点就是子节点的直接上司。

每个职员有一个快乐指数，用整数 Hi 给出，其中 1≤i≤N。

现在要召开一场周年庆宴会，不过，没有职员愿意和直接上司一起参会。 在满足这个条件的前提下，主办方希望邀请一部分职员参会，使得所有参会职员的快乐指数总和最大，求这个最大值。

输入格式 第一行一个整数 N。

接下来 N 行，第 i 行表示 i 号职员的快乐指数 Hi。

接下来 N−1 行，每行输入一对整数 L,K，表示 K 是 L 的直接上司。

输出格式 输出最大的快乐指数。

数据范围 1≤N≤6000, −128≤Hi≤127

Dp:

  • 状态表示f(u, 0 / 1)

    • 集合
      • f(u,0)所有从以u为根的子树中选择，并且不选u这个点的方案
      • f(u,1)所有从以u为根的子树中选择，并且选择u这个点的方案
    • 属性：Min

  • 状态计算(设u的子节点为si)

    f(u, 0) = sum(max(f(si, 0), f(si, 1)))

    f(u, 1) = sum(f(si, 0))

复杂度：O(n)（状态数：2n，所有节点儿子的数量（总枚举次数：n-1）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import java.util.Scanner;

public class Main{
    static int N = 6010;
    static int[][] f = new int[N][2];
    static int[] happy = new int[N];
    static int[] h = new int[N];
    static int[] e = new int[N];
    static int[] ne = new int[N];
    static int idx = 1;
    static boolean[] has_father = new boolean[N];//寻根
    
    static void add(int a, int b){//a父节点 b子节点
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx ++;
    }
    
    static void dfs(int u){
        f[u][1] = happy[u];
        
        for(int i = h[u]; i != 0; i = ne[i]){
            int j = e[i];
            dfs(j);
            f[u][0] += Math.max(f[j][0], f[j][1]);
            f[u][1] += f[j][0];
        }
    }
    
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        for(int i = 1; i <= n; i++)happy[i] = sc.nextInt();
        for(int i = 1; i < n; i++){
            int a = sc.nextInt();
            int b = sc.nextInt();
            add(b, a);//注意顺序
            has_father[a] = true;
        }
        int root = 1;
        while(has_father[root])root++;
        
        dfs(root);
        System.out.println(Math.max(f[root][0], f[root][1]));
    }
}

记忆化搜索

滑雪

Dp:

  • 状态表示f(i, j)

    • 集合
      • 所有从(i, j)开始滑的路径
    • 属性：Max

  • 状态计算(设u的子节点为si)

    集合划分：按第一步滑动方向分成四种

    f[x][y] = Math.max(f[x][y], dfs(nx, ny) + 1);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import java.io.*;

public class Main{
    static int N = 310;
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static int[][] a = new int[N][N];
    static int[][] f = new int[N][N];
    static int[] dx = {-1, 0, 1, 0};
    static int[] dy = {0, 1, 0, -1};
    static int n, m;
    
    static int dfs(int x, int y){
        if(f[x][y] != 0)return f[x][y];//记忆化搜索
        f[x][y] = 1;//记得初始化
        for(int i = 0; i < 4; i++){
            int nx = x + dx[i];
            int ny = y + dy[i];
            if(nx > 0 && ny > 0 && nx <= n && ny <= m && a[x][y] > a[nx][ny]){
                f[x][y] = Math.max(f[x][y], dfs(nx, ny) + 1);
            }
        }
        return f[x][y];
    }
    
    
    public static void main(String[] args) throws IOException{
        String[] str = br.readLine().split(" ");
        n = Integer.parseInt(str[0]);
        m = Integer.parseInt(str[1]);
        for(int i = 1; i <= n; i++){
            str = br.readLine().split(" ");
            for(int j = 1; j <= m; j++){
                a[i][j] = Integer.parseInt(str[j - 1]);
            }
        }
        
        int max = 0;
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= m; j++)
                max = Math.max(max, dfs(i, j));
        
        System.out.println(max);
    }
}