神经网络概念
训练神经网络
构建神经网络
评估模型的技巧
模型修正的技巧
数据迁移
倾斜数据集的误差度量

神经网络

Neural networks

speech -> images -> text(NLP) -> forecast

比较：

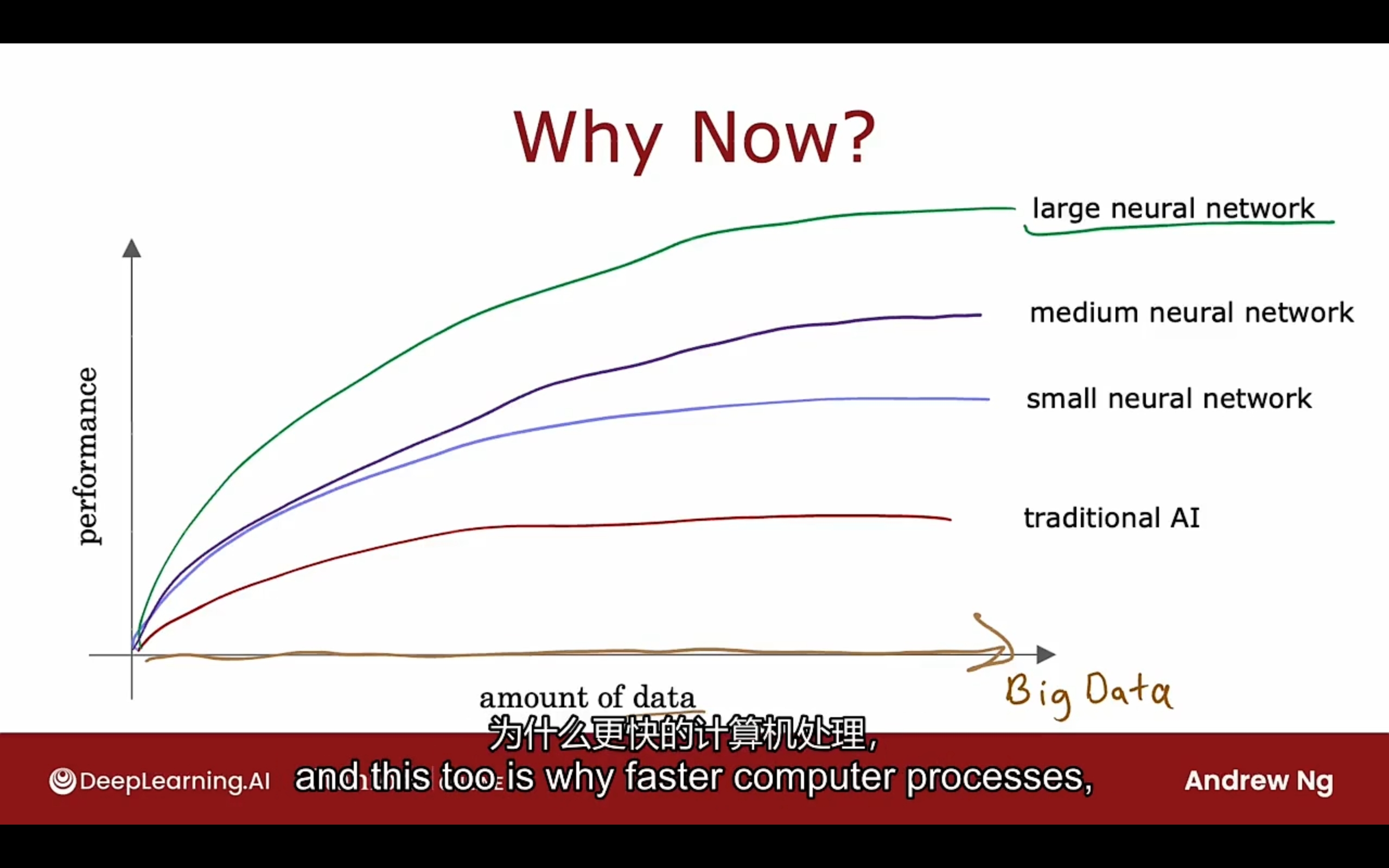
概念

神经网络栗子：

input layer
hidden layer -> activation values
output layer

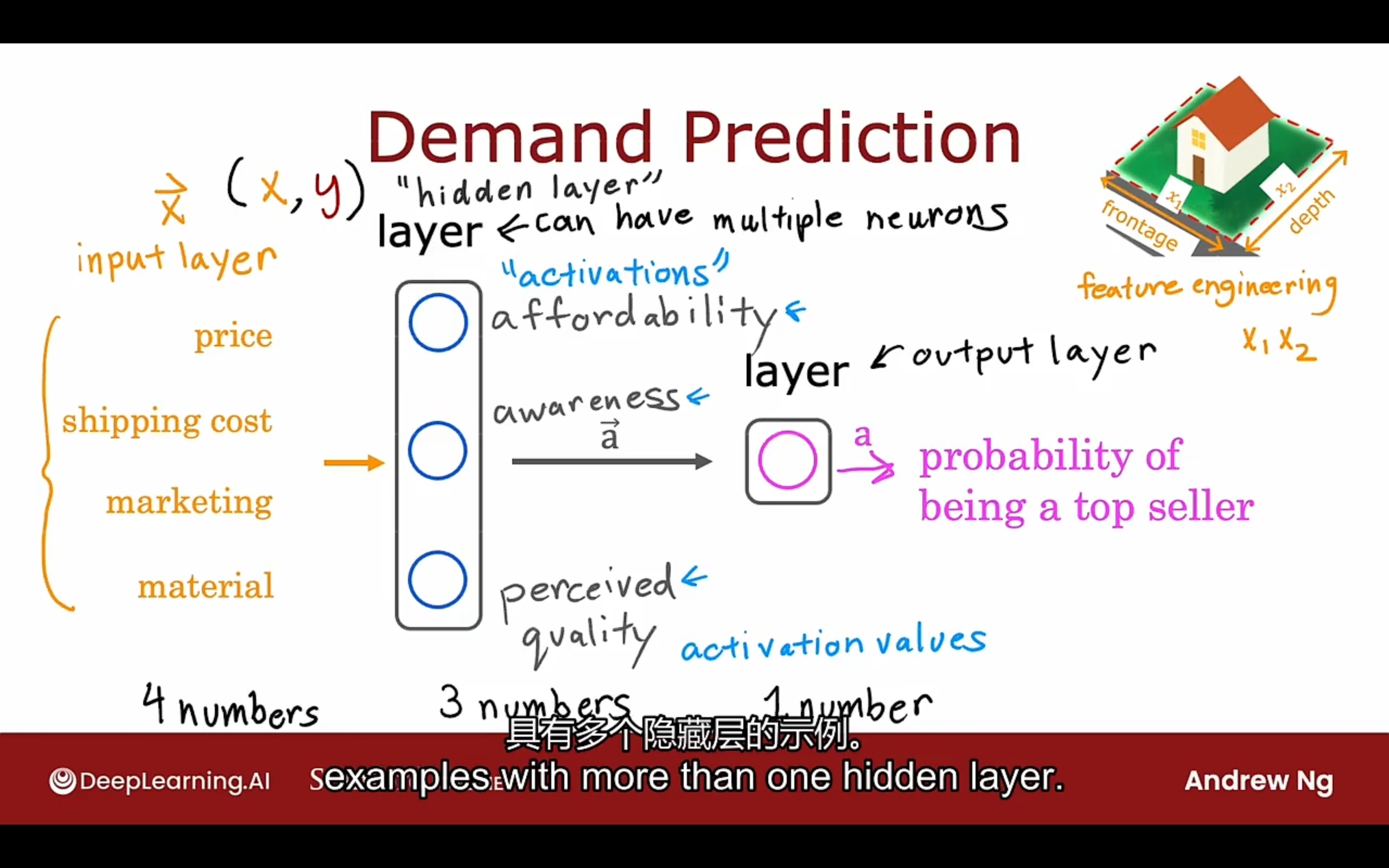
前面的四个特征经过特征工程变成了新的3个特征

神经网络所做的是提炼自己的特征值（在隐藏层中），而不是人为手动的设计

需要决定的点是神经网络的架构：

隐藏层的数量
每个隐藏层中神经元的数量

上下标事项：

layer 1：

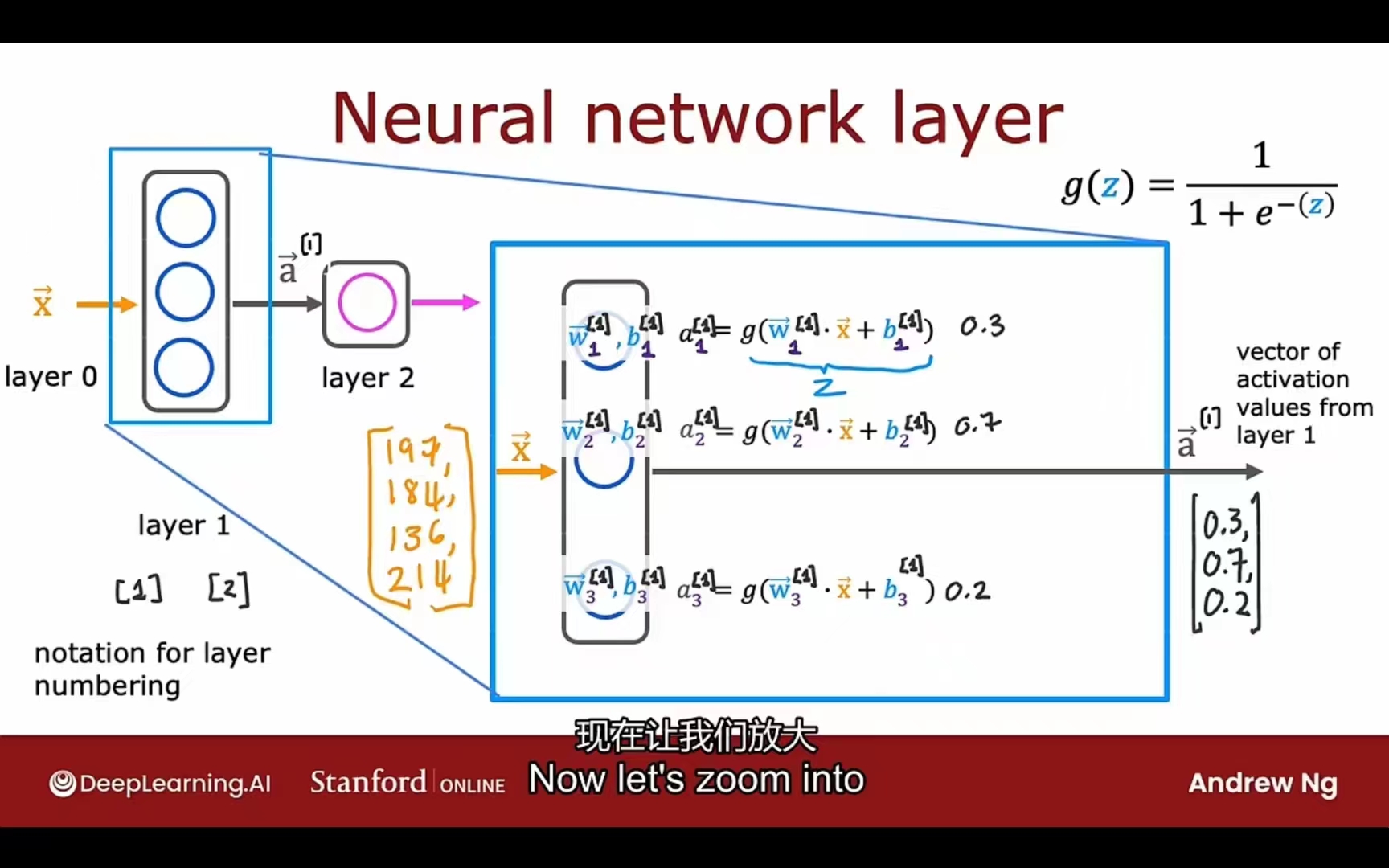
layer 2：

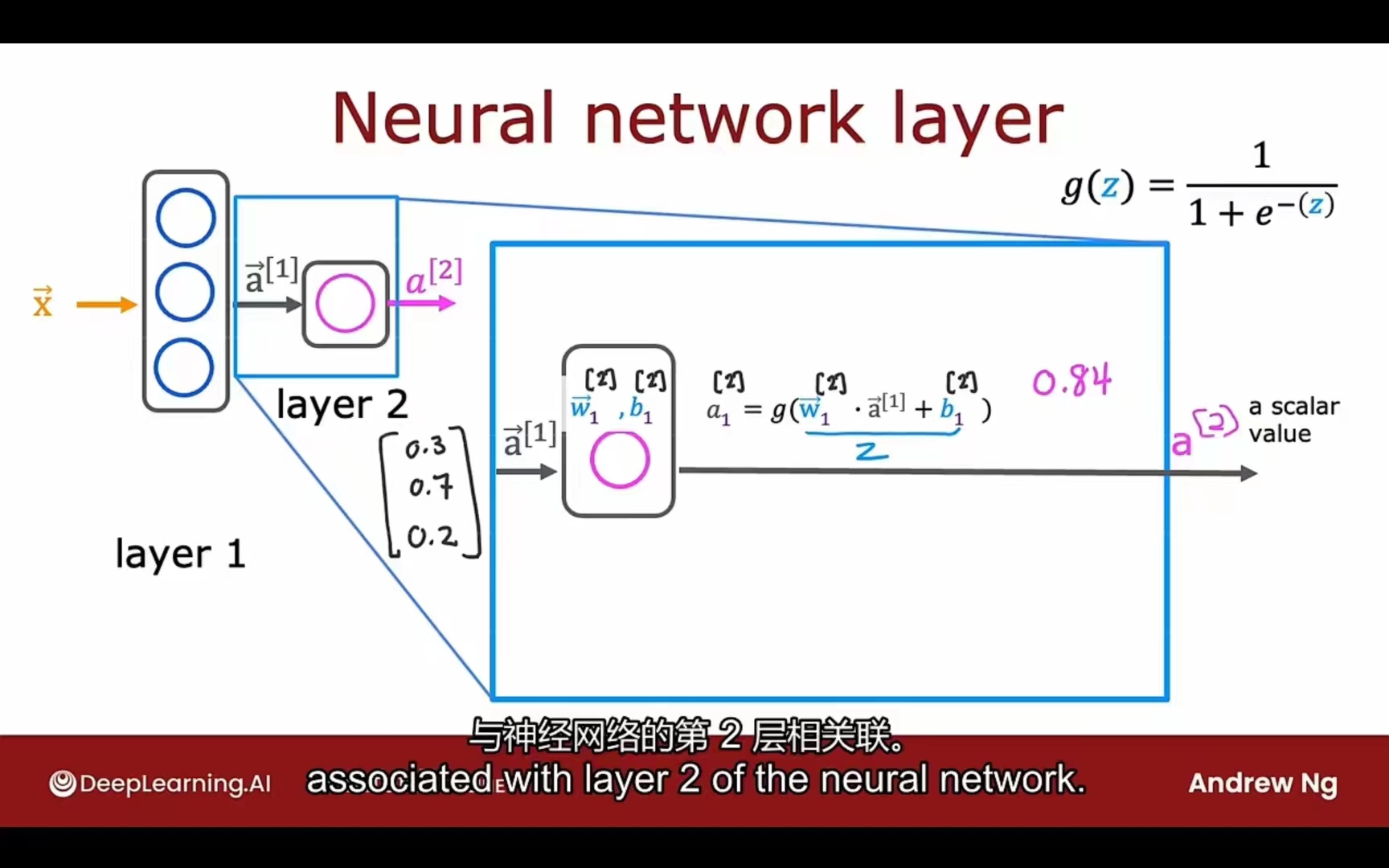
上标：层号

下标：层中神经元号

layer l的第j个神经元的激活函数：

$a^{[l]}_j = g(\vec w_j^{[l]} \cdot \vec a ^ {[l - 1]} + b_j^{[l]})$

g -> sigmoid (also called activation function 激活函数)

PS：输入层可以是 $\vec x = a^{[0]}$

前向传播

forward propagation

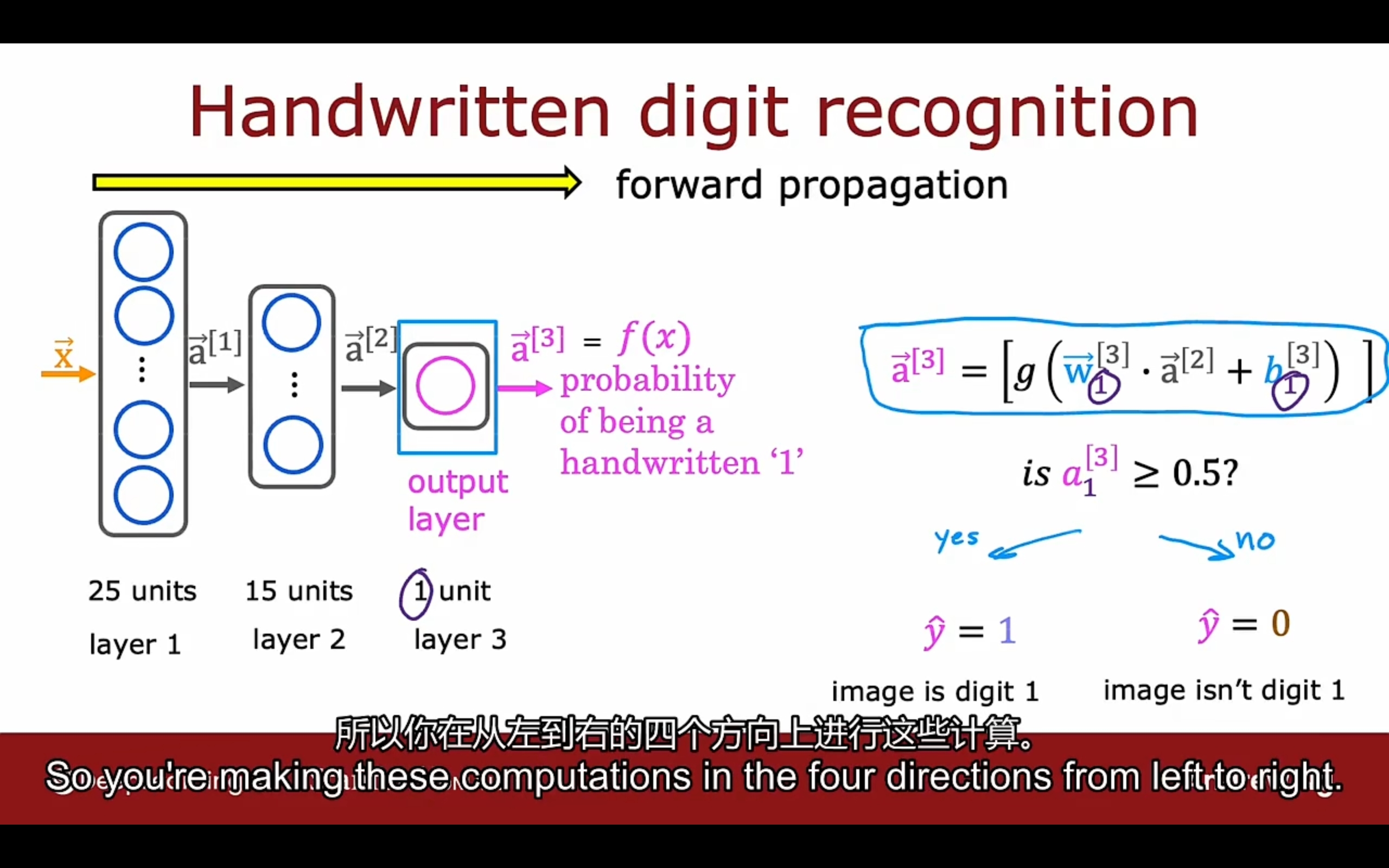
tensorflow实现

x = np.array([200.0, 17.0])
layer_1 = Dense(units=3, activation='sigmoid')
a1 = layer_1(x)

layer_2 = Dense(units=1, activation='sigmoid')
a2 = layer_2(a1)

if a2 >= 0.5
    yhat = 1
else:
    yhat = 0

数据结构

x = np.array([[200, 17]])  # [200, 17] 1 * 2  矩阵 tensorflow中使用
x = np.array([200], [17])  # [200,  矩阵 tensorflow中使用
						   #  17] 2 * 1
x = np.array([200, 17])  # 1D "vector" 线性、逻辑回归中用

x.numpy()  # tensorflow matrix -> numpy array

tensorflow的设计与发明旨在处理非常大的数据集，所以通过在矩阵而不是一维数组中表示数据

所以转换的时候需要注意！

搭建神经网络

layer_1 = Dense(units=3, activation='sigmoid')
layer_2 = Dense(units=1, activation='sigmoid')

model = Sequential([layer_1, layer_2])
x = np.array([200.0, 17.0],
			[120.0, 5.0],
			[425.0, 20.0],
			[212.0, 18.0])
y = np.array([1, 0, 0, 1])
model.complie(...)
model.fit(x, y)

model.predict(x_new)

原理 glance

前向传播的一般实现：

人类大脑具有惊人的适应性和可塑性，去处理不同输入范围、不同种类的信息。

小结论：

如果当前层的输入为$s_{in}$个单元，输出为$s_{out}$个单元，那么$\vec w$ 将是$s_{in} * s_{out}$的矩阵
b将是一个$s_{out}$的向量

补充知识：

向量点乘和矩阵乘法的关系：

$\vec a \cdot \vec w = \vec a^T \vec w$

a_in是(m, n)，W是(n, j), b是(j, 1)的向量

矩阵乘法会加速训练过程

def dense(A_in, W, b, g)
	# A的转置 A.T
	z = np.matmul(A_in, W) + b  # 矩阵乘法(m, n)(n, j) = (m, j)
	A_out = g(z)
    return A_out

其中b能加不报错的原因：

训练神经网络(多层感知机)的细节

import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.losses import BinaryCrossentropy

model = Sequential([
	Dense(units=25, activations='sigmoid'),
    Dense(units=10, activations='sigmoid'),
    Dense(units=1, activations='sigmoid')
])
x = np.array([200.0, 17.0],
			[120.0, 5.0],
			[425.0, 20.0],
			[212.0, 18.0])
y = np.array([1, 0, 0, 1])

model.complie(loss=BinaryCrossentropy())

model.fit(x, y, epochs=100)  # epoch: number of steps in gradient descent

model.predict(x_new)

better version：

import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.losses import BinaryCrossentropy

model = Sequential([
	Dense(units=25, activation='sigmoid'),
    Dense(units=10, activation='sigmoid'),
    Dense(units=1, activation='linear')  # 线性输出
])
x = np.array([200.0, 17.0],
			[120.0, 5.0],
			[425.0, 20.0],
			[212.0, 18.0])
y = np.array([1, 0, 0, 1])

model.complie(loss=BinaryCrossentropy(from_logits=True))

model.fit(x, y, epochs=100)  # epoch: number of steps in gradient descent

# predict
logit = model(x_new)
f_x = tf.nn.sigmoid(logit)
model.predict(x_new)

损失函数：

BinaryCrossentropy() 二元交叉熵损失函数
MeanSquareError() 均值方差损失函数

激活函数：

sigmoid

$g(z) = \frac{1}{1 + e^{-z}}$
- 适用范围：y = 0 / 1
ReLU (most common)

$g(z) = max(0, z)$
- 适用范围： y = + / -
- 优势：相较于sigmoid往往训练得更快（因为梯度下降flat的地方很少）
Linear activation function 线性激活函数(相当于没用)

$g(z) = z$
- 适用范围：y = 0 or +
Softmax
LeakyReLU
tan h
swish

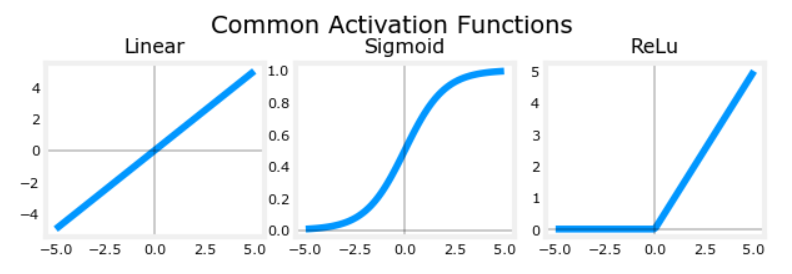
建议：

输出层：
- sigmoid y = 0 / 1 二分类问题
- linear y = + / -
- ReLU y = 0 or +
隐藏层：
- ReLU

使用激活函数的必要性：

如果所有层（hidden + output) 的激活函数都是线性激活函数（或没有激活函数），那么其等价于一个线性回归模型；

如果hidden层的激活函数都是线性激活函数（或没有激活函数），output层的激活函数是sigmoid，那么其等价于一个逻辑回归模型

so, hidden层不要全部使用linear activation function!

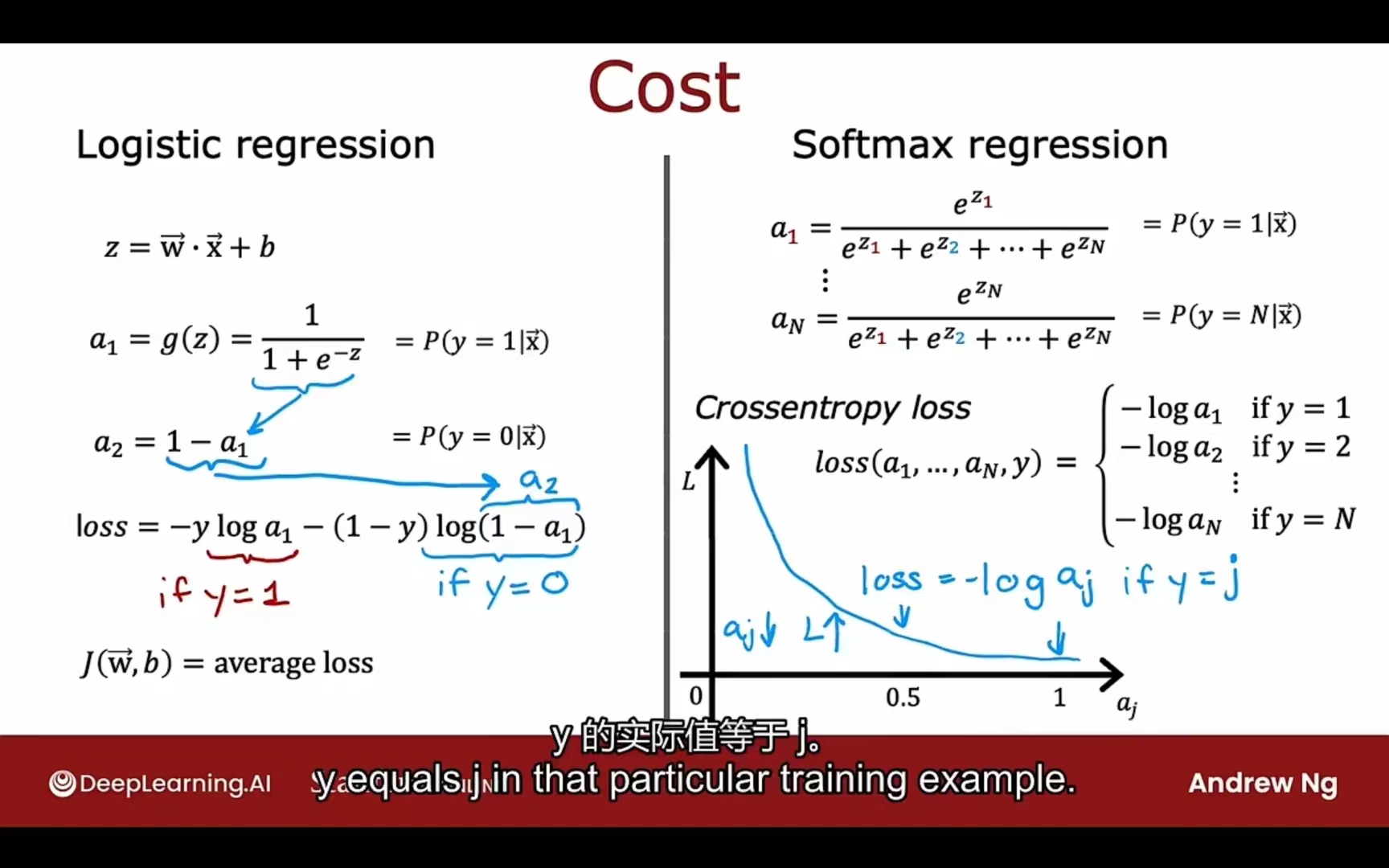
Softmax

公式：

$z_j = \vec w_j \cdot \vec x + b_j \\ j = 1, ..., N$ $a_j = \frac{e^{z_j}}{\sum_{k=1}^{N}e^{z_k}} = P(y=j|\vec x) \\ a_1 + a_2 + ... + a_N = 1$

成本函数：

$loss(a_1,...,a_N,y) = \begin{equation} \left\{ \begin{array}{lr} -loga_1 & if \ y = 1 \\ -loga_2 & if \ y = 2 \\ ... \\ -loga_n & if \ y = N \end{array} \right. \end{equation}$

implement in code：

import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.losses import SparseCategoricalCrossentropy

model = Sequential([
	Dense(units=25, activation='relu'),
    Dense(units=15, activation='relu'),
    Dense(units=10, activation='softmax')
])
# 多分类交叉熵损失函数
model.complie(loss=SparseCategoricalCrossentropy())

model.fit(x, y, epochs=100)

model.predict(x_new)

better version（改进实现）：

import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.losses import SparseCategoricalCrossentropy

model = Sequential([
	Dense(units=25, activations='relu'),
    Dense(units=15, activations='relu'),
    Dense(units=10, activations='linear')
])

model.complie(loss=SparseCategoricalCrossentropy(from_logits=True))

model.fit(x, y, epochs=100)

logits = model(X)
preferred = tf.nn.softmax(logits).numpy()
for i in range(len(preferred)):
    print(f"{preferred[i]}, category: {np.argmax(preferred[i])}")

原理相同，但在数字计算层面更精准（直接带入，tensorflow自动优化）

Softmax函数的准确计算：

原理：

$a_j = \frac{e^{z_j - C}}{\sum_{i=1}^{N}e^{z_i - C}} \ \ \ \ \ where \ C = max_j(z)$

可有效防止指数过大的溢出(overflow)现象

def my_softmax_ns(z):
    """numerically stablility improved"""
    bigz = np.max(z)
    ez = np.exp(z-bigz)              # minimize exponent
    sm = ez/np.sum(ez)
    return(sm)

交叉熵损失函数的准确计算：

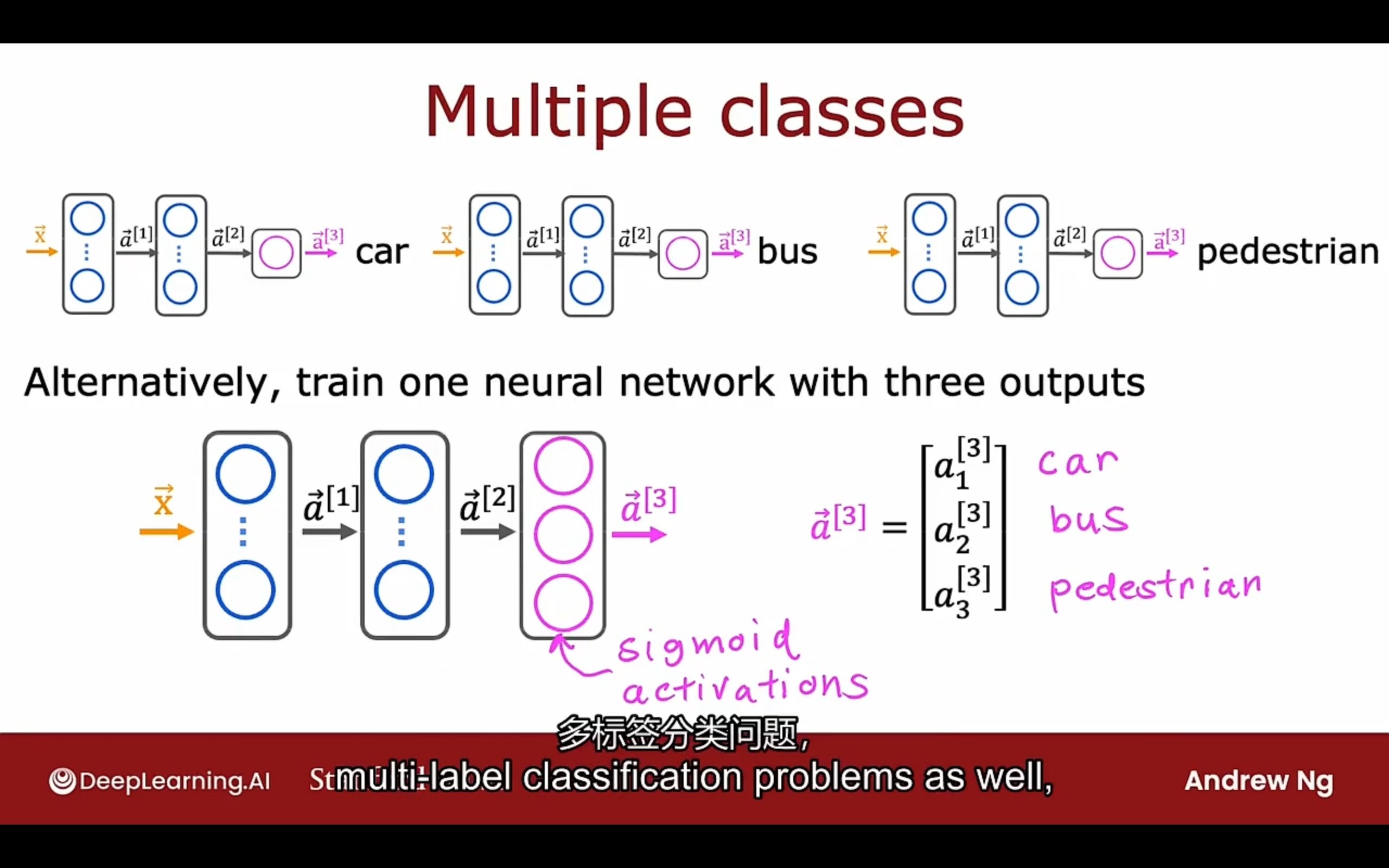
多输出(标签)问题

Adam优化器

Adam optimizers

可以自动调整学习率

对每个参数都有自己的学习率

如果$w_j$ or b保持向同样一个方向移动，就加大学习率$\alpha_j$
如果$w_j$ or b持续震荡或弹跳，就缩减学习率$\alpha_j$

implement code：

1 2	model.complie(optimizer=tf.keras.optimizers.Adam(learning_rate=1e-3)), loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True))

layer分类

Dense Layer 全连接层

Each neuron output is a function of all the activation outputs of the previous layer

主要用于网络的最后一层，负责将前面提取到的特征进行分类和回归
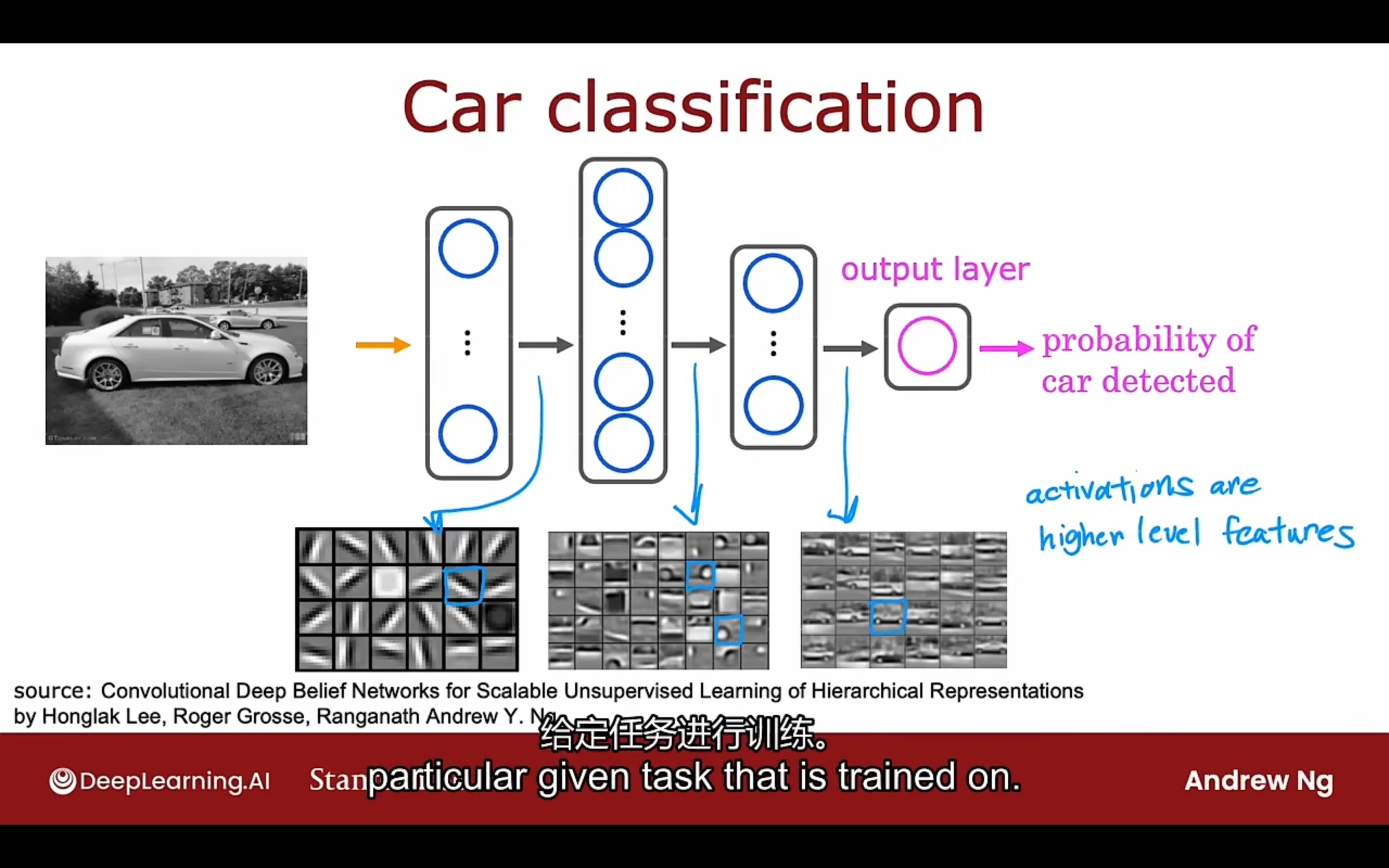
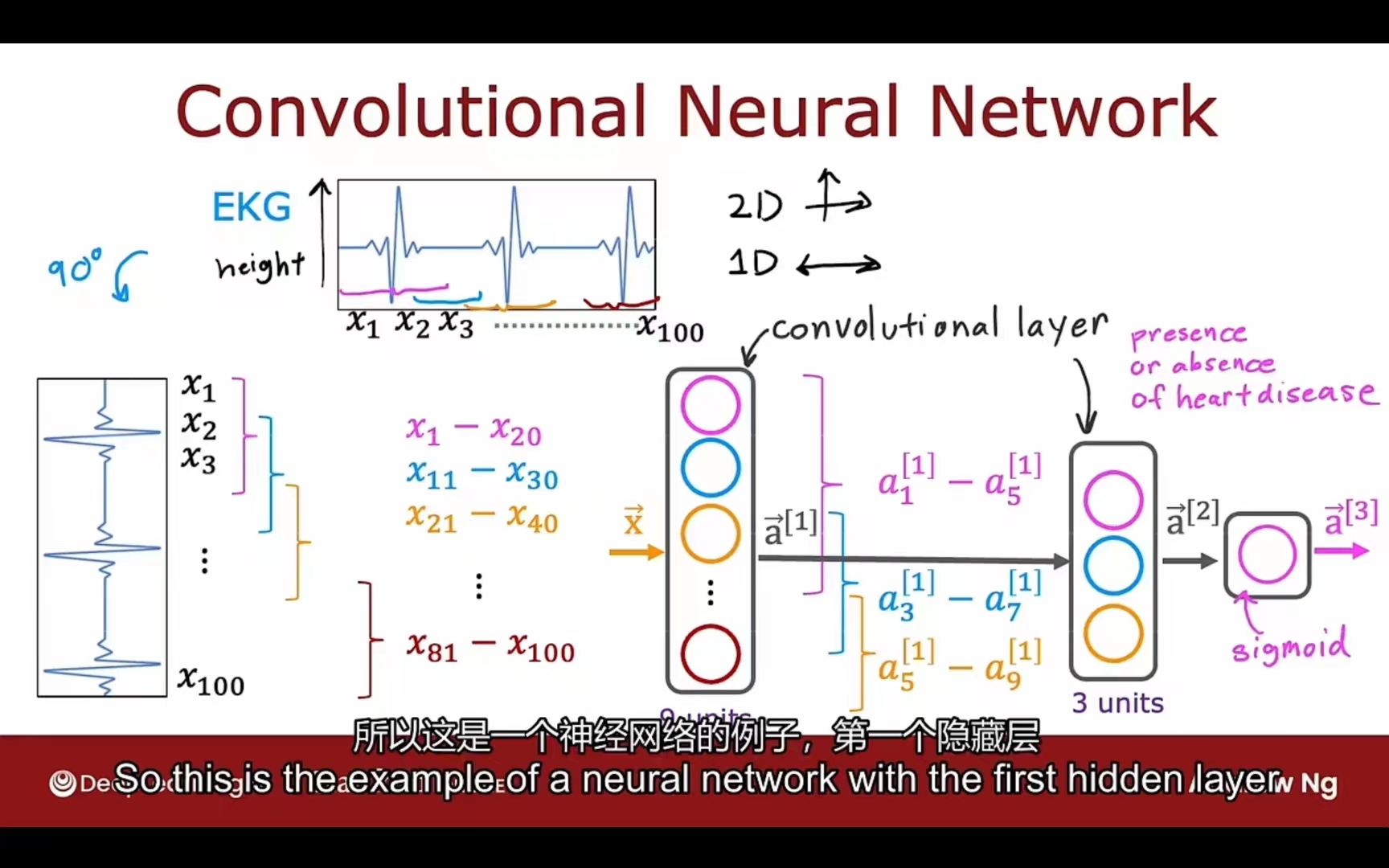
Convolutional Layer 卷积层

Each neuron only looks at part of the previous layer’s inputs

主要用于提取数据的特征

优点：
- 更快的计算速度
- 更少的训练数据需求（不易过拟合）
CNN范例：

PS： Python中导数求法

需要库sympy

import sympy
J, w = sympy.symbols('J, w')
J = w ** 2
w_2
dj_dw = syspy.diff(J, w)  # 求导
2w
dt_dw.subs([(w, 2)])  # 代入
4

从左到右计算损失函数前向传播
从右到左计算导数反向传播

参考：https://blog.csdn.net/ft_sunshine/article/details/90221691

tips

增大训练集
减少特征值
获取额外的特征
增加高次幂特征
增大、减小正则化系数

评估模型

划分数据集：

方式一：

70% 训练集

30% 测试集

针对均方误差：

针对逻辑回归：

对于分类问题，还可以统计测试集被错误分类的比例

implement code:

1	X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.33, random_state=1) # 2:1 打乱顺序

方式二：

60% 训练集
20% 交叉验证集(验证集 / 开发集) cross validation / development set
20% 测试集

训练集用于训练模型
验证集用于选取模型（选取最小损失的多项式或神经网络结构）
测试集用于测试模型泛化能力

implement code:

1
2
3

# train:cv:test=0.6:0.2:0.2
X_train, X_, y_train, y_ = train_test_split(X,y,test_size=0.40, random_state=1)
X_cv, X_test, y_cv, y_test = train_test_split(X_,y_,test_size=0.50, random_state=1)

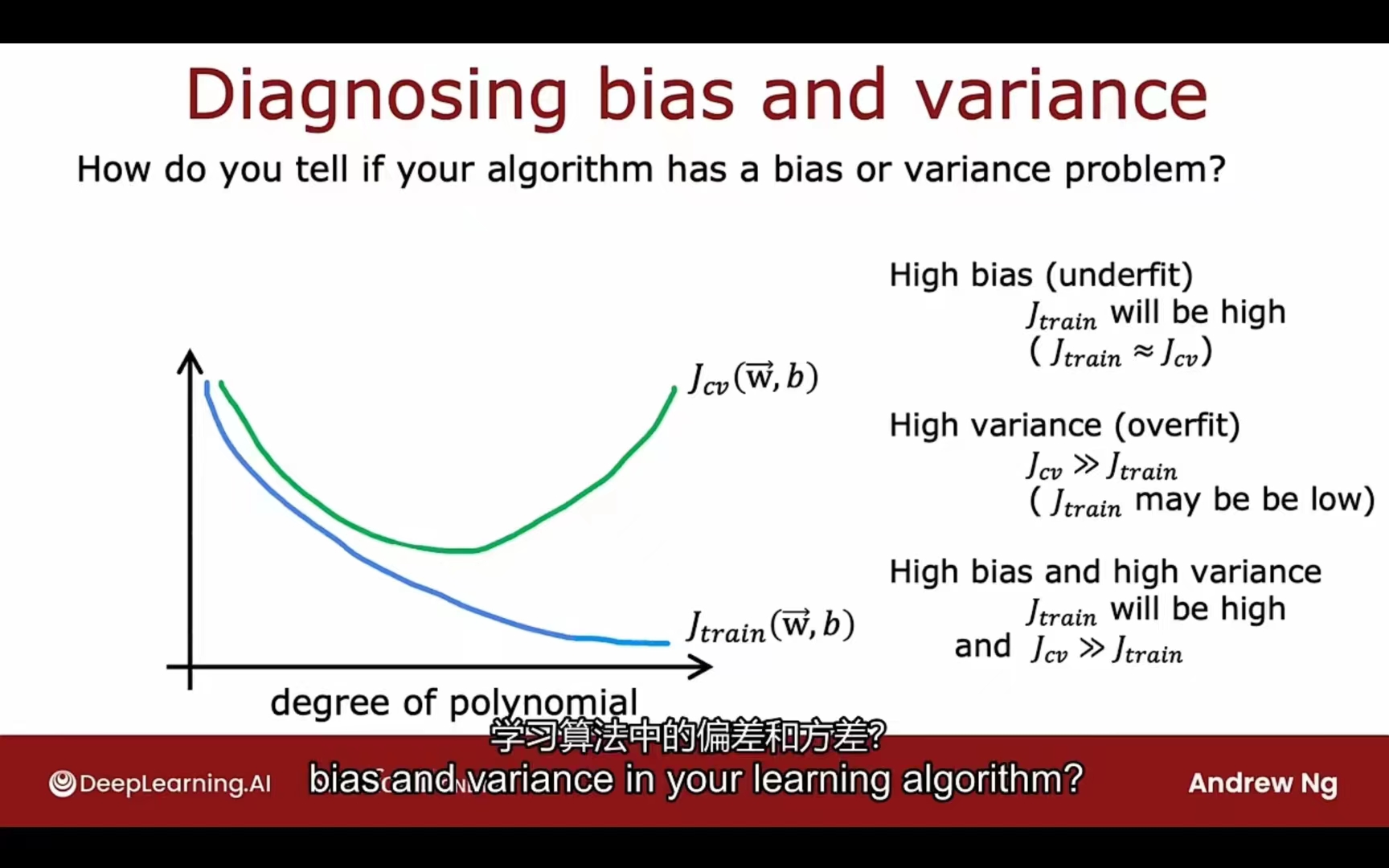
结合偏差和方差

$J_{train}$ 偏大 -> 模型欠拟合（high bias）

$J_{train}$小，但$J_{cv}$ 偏大 -> 模型过拟合（high variance）

$J_{train}$ 小，$J_{cv}$相较于$J_{train}$也偏小 -> just right

正则化系数

左侧过拟合，右侧欠拟合

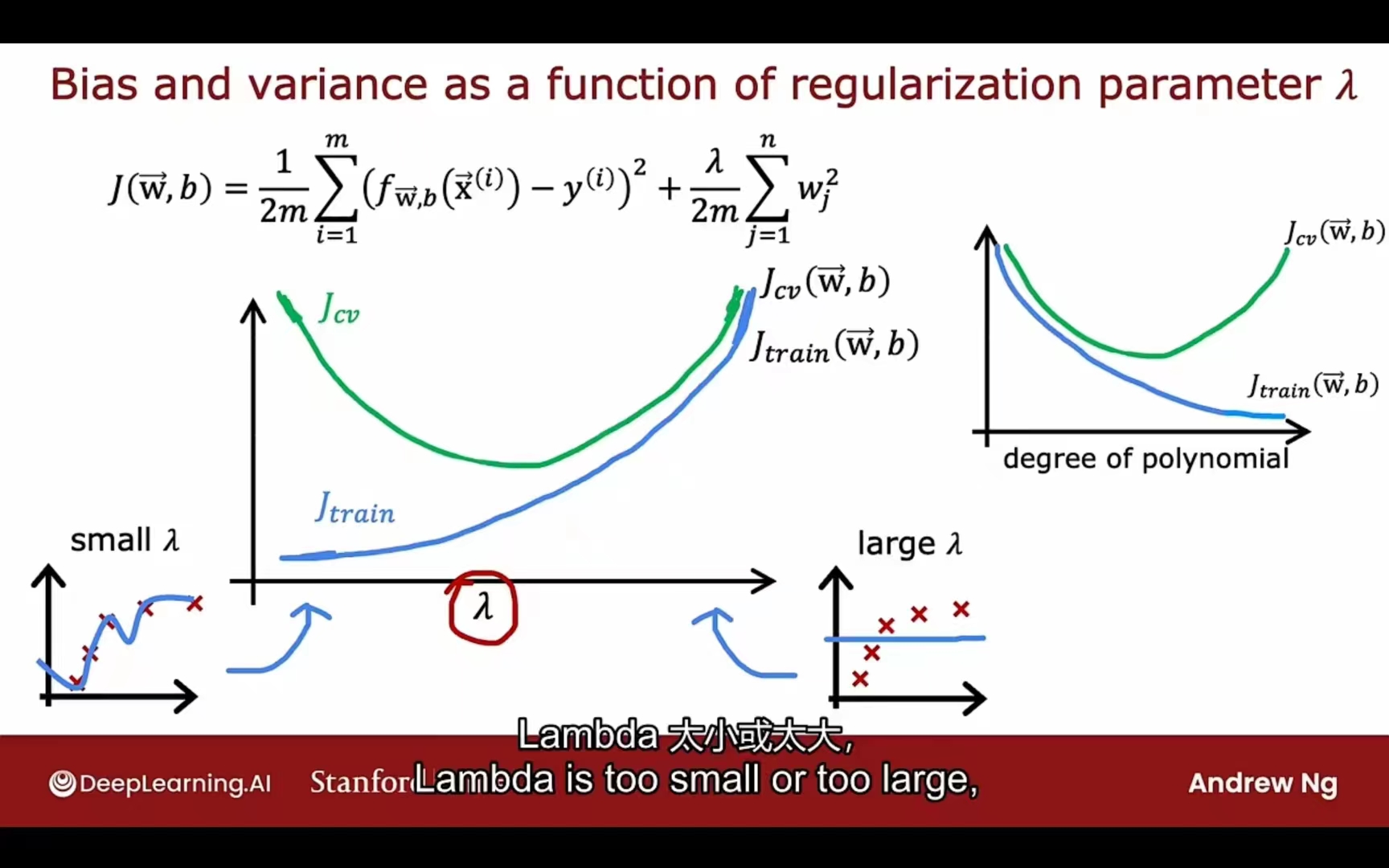
所以通过$J_{train}$ 和$J_{cv}$可以帮助$\lambda$的选择

如何判断J的水平是高的？ -> benchmark

人类的表现水平
同类竞争性算法表现
通过经验推断

学习曲线

high bias：

high variance：

总结

增加特征数量（high bias）
增加高次幂特征（high bias）
减小正则化系数（high bias）

增大训练集（high variance)
减少特征数量（high variance）
增大正则化系数（high variance）

The knowledge above takes short time to learn, but life time to master.

神经网络的修正

训练、调试的循环

特色：只要正则化方式合适，一个大规模的神经网络通常会比一个小的神经网络表现更好（更小概率出现过拟合现象）代价：计算量更大，训练更慢

1	layer_1= Dense(units=25, activation="relu", kernel_regularizer=L2(0.01))

PS:

L1：参数绝对值
L2：参数平方
L3： L1 + L2

数据添加的技巧

添加一些有侧重性的数据
改变现存数据变为新数据（图像放缩、扭曲、反转、噪点；语音噪音增加、损失、失真）
数据生成

AI = Code + Data

数据迁移

监督预训练 Supervised Pre-training
微调 Fine tuning

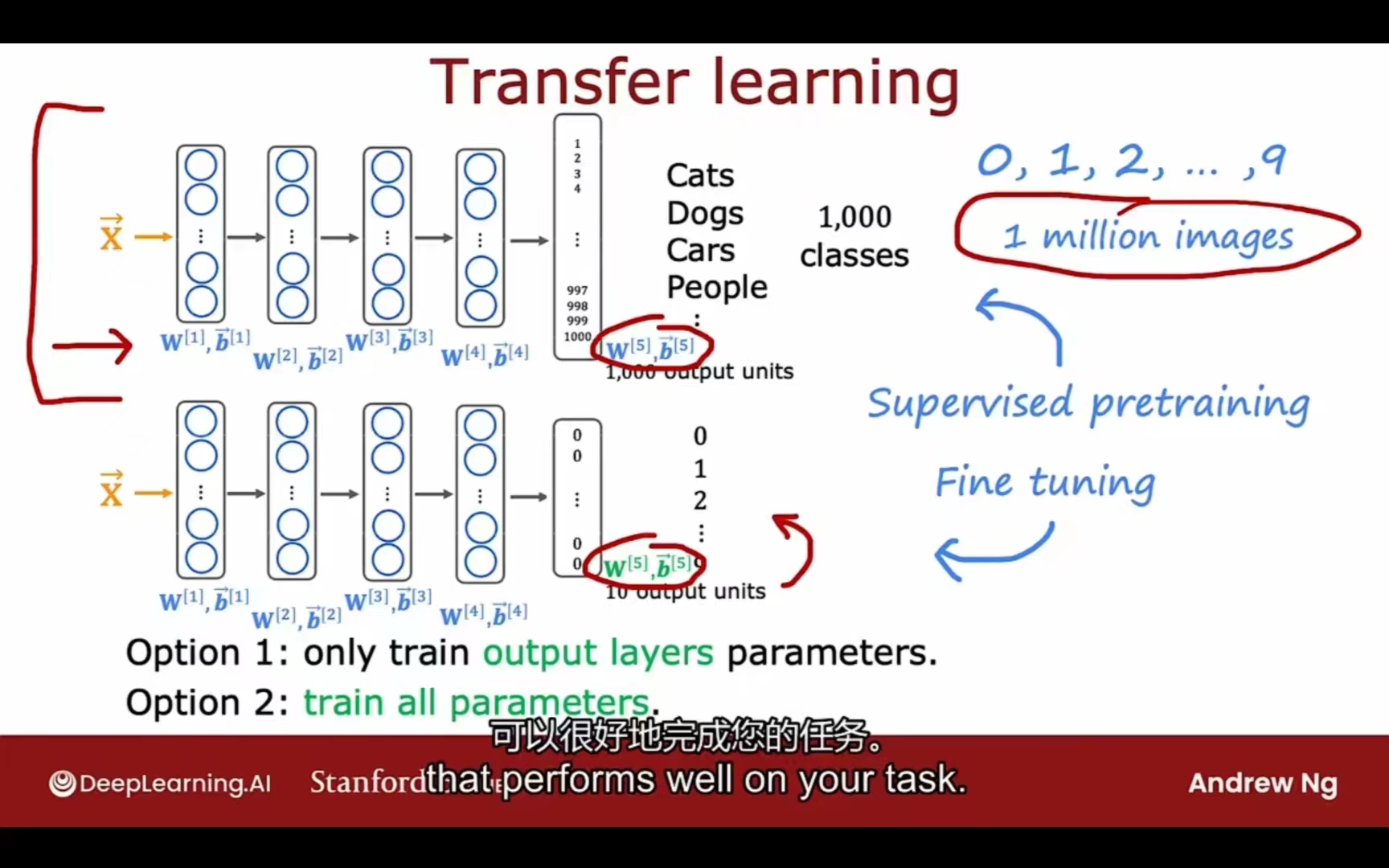
只训练自己的最后层的参数
训练全部参数（拿之前的模型参数做初始化）

误差度量(倾斜数据集)

精确率 Precision

预测为1的多少是实际为1

precision = true positives / total predicted positive
召回率 Recall

实际为1的多少是预测为1

recall = true positives / total actual positive

两者的权衡：

根据实际情况：

如果预测为1需要很谨慎

阈值提高（高于0.5）更高精确率，更低召回率
如果预测为1很必要

阈值降低（低于0.5）更低精确率，更高召回率

综合评判：F1 score P和R的调和平均

$F1 \ score = \frac{1}{\frac{1}{2}(\frac{1}{P} + \frac{1}{R})} = 2\frac{PR}{P+R}$

Polaris6G's blog

机器学习-02