学习决策树

概念与计算
搭建过程
独热码
回归树
集成学习
- 随机森林
- 提升树
与神经网络的比较
代码实现

概念

树：

根节点
决策节点
叶节点

决策树学习算法的工作：在所有的可能决策树中尝试选择一个希望在训练集表现良好的情况下，在推广数据集（交叉验证集、测试机）中同样如此的理想决策树模型。

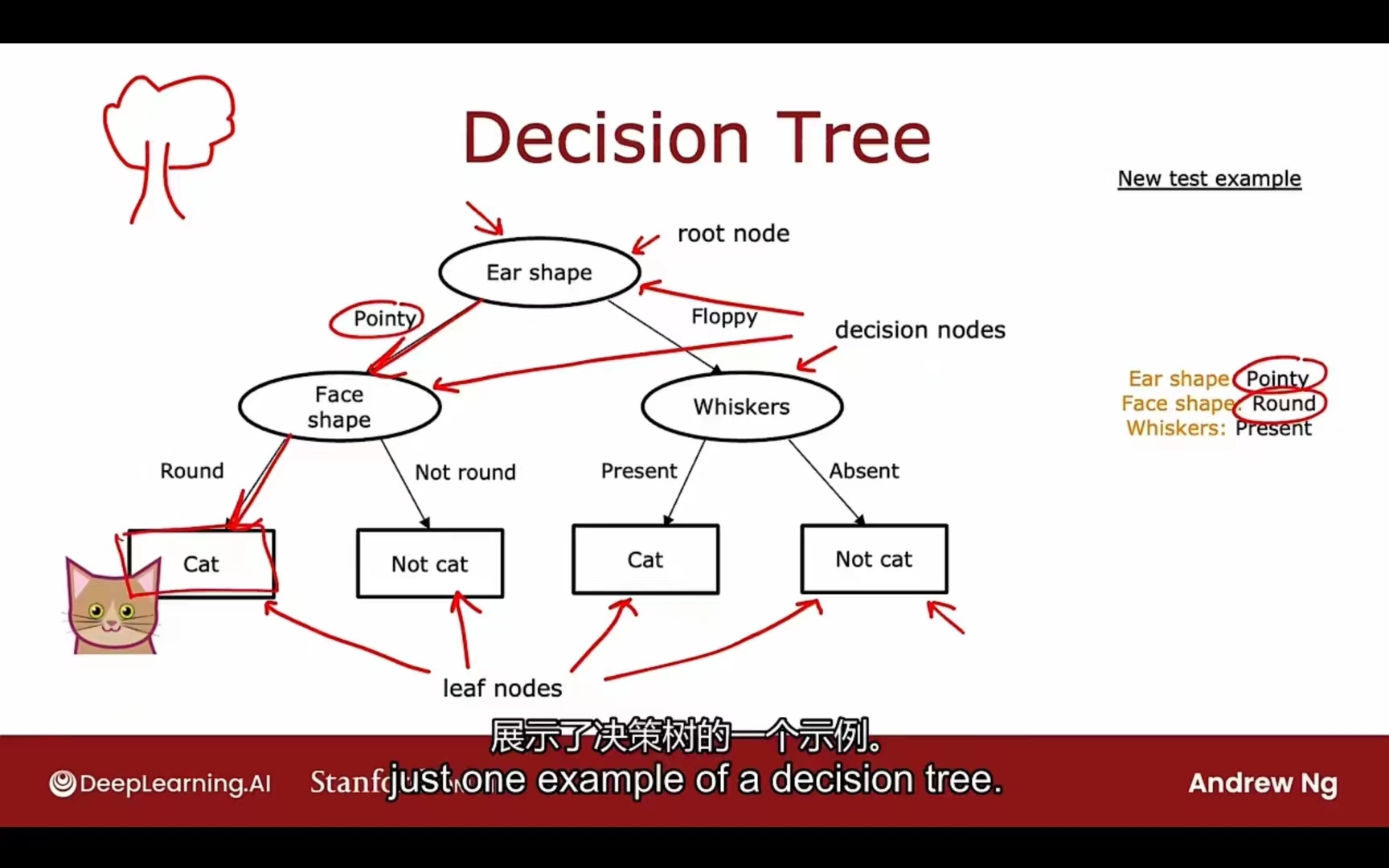
关键点

如何选择哪个特征去区分每个节点

依据最大纯度 -> 熵
什么时候停止划分
- 当一个节点全为1类
- 当划分该节点时会导致树的最大深度增加（防止树变复杂过拟合）
- 纯度分数的提升低于阈值
- 节点中某类的数量低于阈值

衡量纯度

熵函数：

H(0) = 0
H(1) = 0
H(0.5) = 1

$p_0 = 1 - p_1$ $H(p_1)=-p_1log_2(p_1) - p_0log_2(p_0) \\ = -p_1log_2(p_1) - (1 - p_1)log_2(1-p_1)$

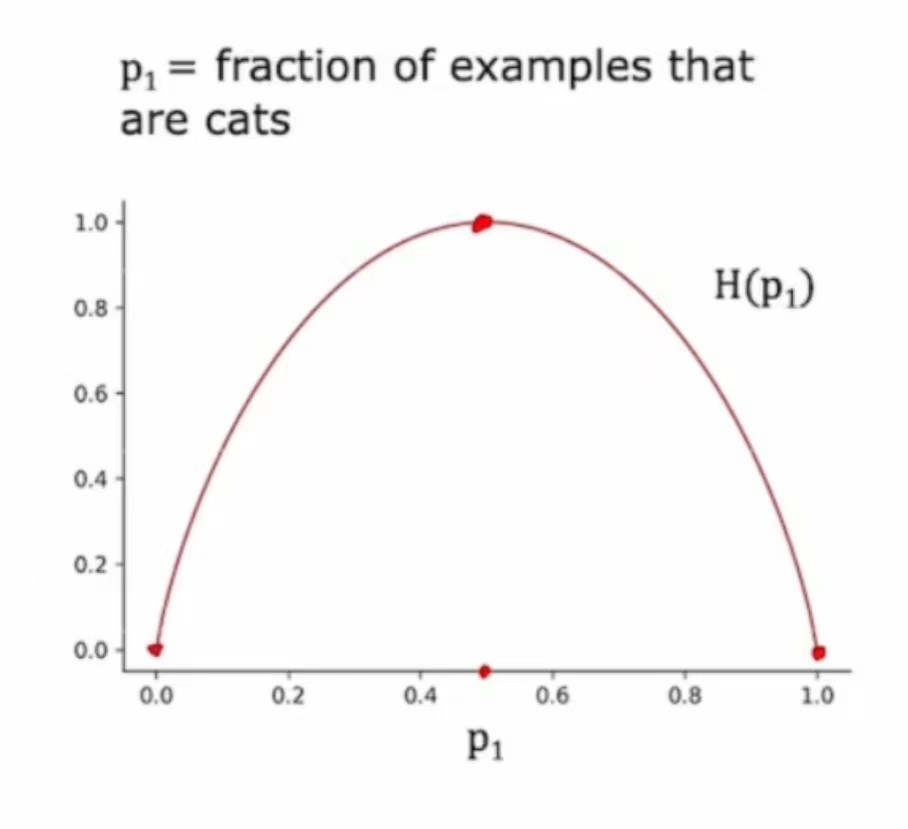
熵的减少被称为信息增益

选择特征的依据：最低加权平均熵

栗子：

可以给出信息增益的公式：

$Information\ gain = H(p_1^{root}) - (w^{left}H(p_1^{left})+w^{right}H(p_1^{right}))$

搭建过程

先序遍历：

所有样例从根节点开始
分别计算所有潜在特征的信息增益，从中选出最高的
根据选中的特征划分数据集，创建树的左右枝干
继续划分直到达到停止标准：
- 划分出的数据集纯度100%
- 划分会导致树高超过限制
- 信息增益小于阈值
- 划分子集数量小于阈值

针对连续值特征：

需要考虑每个拆分的标准，根据这个标准计算信息增益，选择信息增益最大的值进行拆分。

上图选择的具体方法是：在10个数据之间的9个空隙中选择中点，分别计算各自的信息增益，选择最高的那个作为分类依据。

独热码

如果一个分类特征有k种分类方式，那么可以创造k个二进制特征（0 or 1）

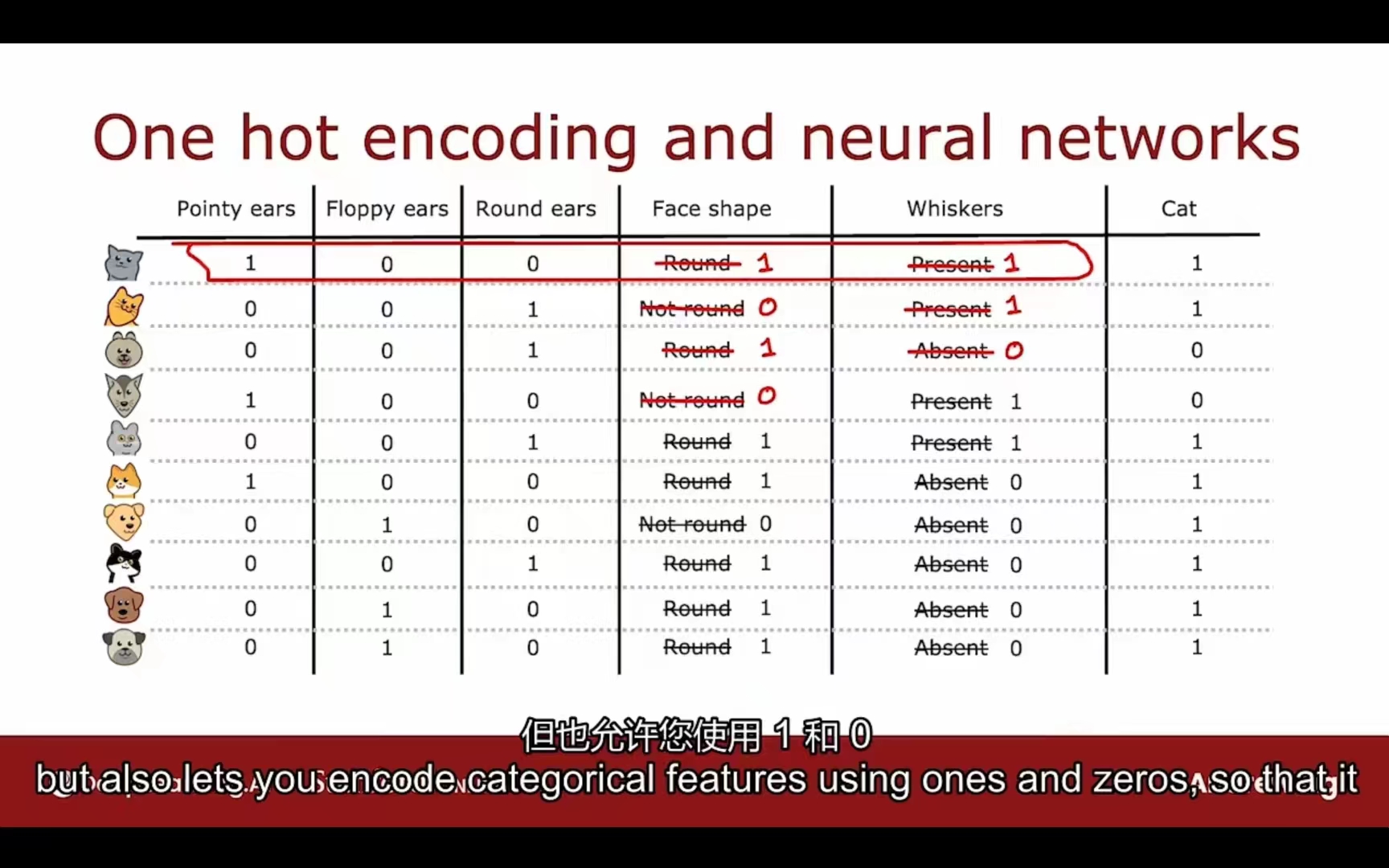
独热码不仅可以用于决策树，也可以用于逻辑回归和神经网络。

注意：独热码只能同时有一个特征为1，其余都为0

回归树

预测数字

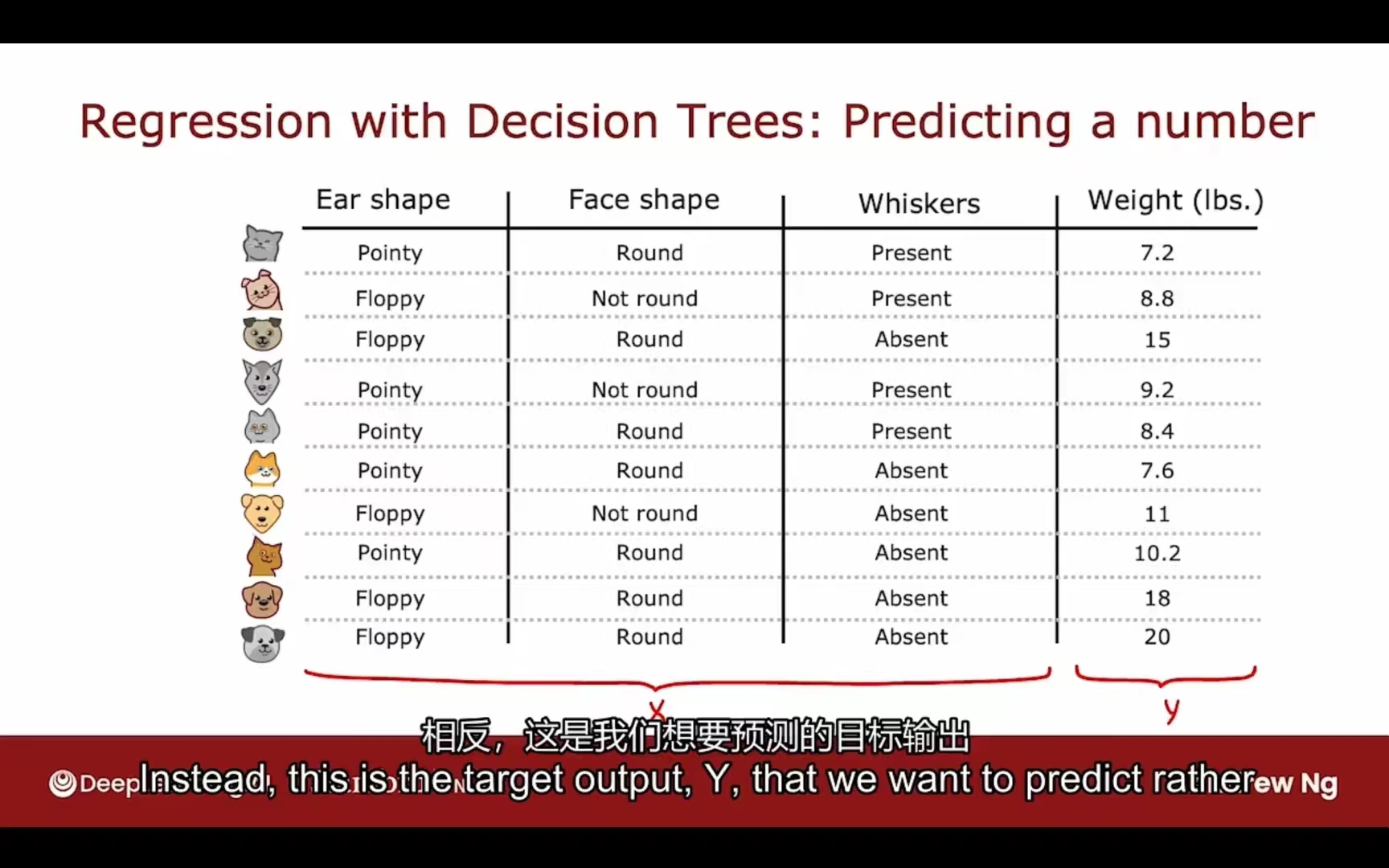
信息增益 -> 测量方差

选择分类特征的过程（类比决策树）

树集合

树对于数据集的改动十分敏感，所以可选择多颗不同类型的决策树加大普适性

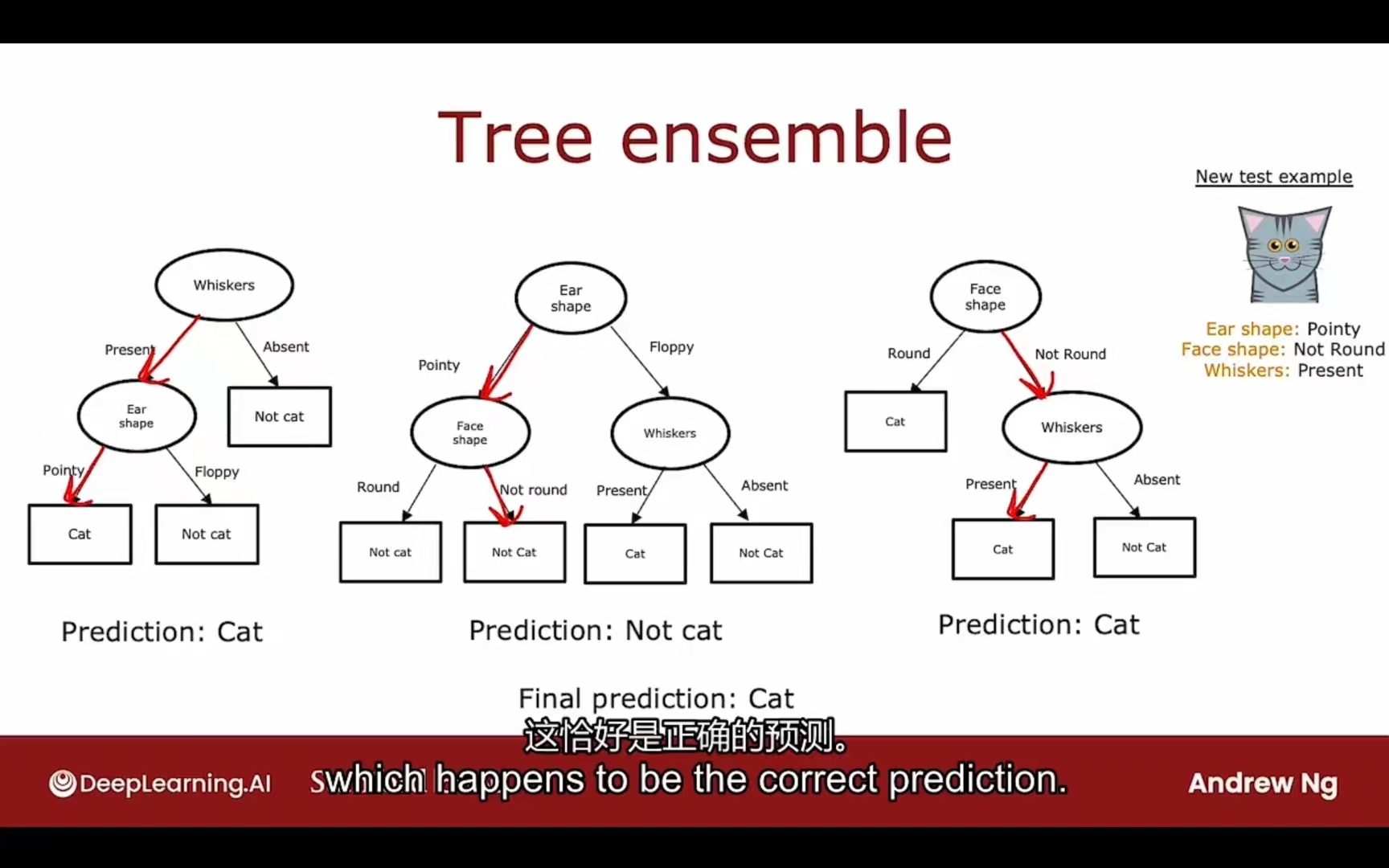
随机森林

random forest 集成学习

前提：新的数据集通过有放回抽样进行

随机森林生成过程：

数据集大小：m

1
2
3

for b = 1 to B:  # B决定随机森林中子树个数
	有放回抽样去创造新的数据集(大小为m)
    根据新数据集训练一颗决策子树

为了使每颗决策子树不同程度高以增加模型普适性，可以采用如下方法：

n个特征划分为随机包含其中k个特征的子集，在子集中进行选择

习惯选择$k=\sqrt{n}$

Boosted trees

提升树

for b = 1 to B:  # B决定随机森林中子树个数
	有放回抽样去创造新的数据集(大小为m)
    	但是更倾向于选择之前决策树错误分类的样例，而不是等概率抽
    根据新数据集训练一颗决策子树

XGBoost

eXtreme Gradient Boosting

提升树的开源实现
非常快捷和高效
有良好的选择默认拆分标准和何时停止拆分的标准
内置了正则化以防止过拟合
是一种算法竞赛中竞争激烈的算法

分类：

from xgboost import XGBClassifier

model = XGBClassifier()

model.fit(X_train, y_train)
y_pred = model.predict(X_test)

回归：

from xgboost import XGBRegressor

model = XGBRegressor()

model.fit(X_train, y_train)
y_pred = model.predict(X_test)

决策树的使用场景

决策树和树的集成学习：

在结构化数据上表现很好（表格等）
不推荐在非结构化数据上使用（图像，音频，文字）
训练真的很快
小型决策树可以人工分析内部

神经网络：

在结构化和非结构化数据上都表现很好
相对决策树训练会更慢
可以和迁移学习一起使用
多个神经网络相互独立可以并发训练，而随机森林只能一个接一个训练

代码实现决策树

熵函数：

def compute_entropy(y):
    """
    Computes the entropy for 
    
    Args:
       y (ndarray): Numpy array indicating whether each example at a node is
           edible (`1`) or poisonous (`0`)
       
    Returns:
        entropy (float): Entropy at that node
        
    """
    # You need to return the following variables correctly
    entropy = 0.
    
    ### START CODE HERE ###
    if len(y):
        p1 = len(y[y==1]) / len(y)
        if p1 != 0 and p1 != 1:
            entropy = -p1 * np.log2(p1) - (1 - p1) * np.log2(1 - p1)
    ### END CODE HERE ###        
    
    return entropy

划分函数：

def split_dataset(X, node_indices, feature):
    """
    Splits the data at the given node into
    left and right branches
    
    Args:
        X (ndarray):             Data matrix of shape(n_samples, n_features)
        node_indices (ndarray):  List containing the active indices. I.e, the samples being considered at this step.
        feature (int):           Index of feature to split on
    
    Returns:
        left_indices (ndarray): Indices with feature value == 1
        right_indices (ndarray): Indices with feature value == 0
    """
    
    # You need to return the following variables correctly
    left_indices = []
    right_indices = []
    
    ### START CODE HERE ###
    
    x = X[:,feature]
    
    for i in node_indices:
        if x[i] == 1:
            left_indices.append(i)
        else:
            right_indices.append(i)
    ### END CODE HERE ###
        
    return left_indices, right_indices

信息增益计算函数：

# UNQ_C3
# GRADED FUNCTION: compute_information_gain

def compute_information_gain(X, y, node_indices, feature):
    
    """
    Compute the information of splitting the node on a given feature
    
    Args:
        X (ndarray):            Data matrix of shape(n_samples, n_features)
        y (array like):         list or ndarray with n_samples containing the target variable
        node_indices (ndarray): List containing the active indices. I.e, the samples being considered in this step.
   
    Returns:
        cost (float):        Cost computed
    
    """    
    # Split dataset
    left_indices, right_indices = split_dataset(X, node_indices, feature)
    
    # Some useful variables
    X_node, y_node = X[node_indices], y[node_indices]
    X_left, y_left = X[left_indices], y[left_indices]
    X_right, y_right = X[right_indices], y[right_indices]
    
    # You need to return the following variables correctly
    information_gain = 0
    
    # Weights 
    w_left = len(X_left) / len(X_node)
    w_right = len(X_right) / len(X_node)
    
    # Entropy
    hp_node = compute_entropy(y_node)
    hp_left = compute_entropy(y_left)
    hp_right = compute_entropy(y_right)
    
    #Information gain                                                   
    
    information_gain = hp_node - (w_left * hp_left + w_right * hp_right)
    
    return information_gain

找最大信息增益的特征：

def get_best_split(X, y, node_indices):   
    """
    Returns the optimal feature and threshold value
    to split the node data 
    
    Args:
        X (ndarray):            Data matrix of shape(n_samples, n_features)
        y (array like):         list or ndarray with n_samples containing the target variable
        node_indices (ndarray): List containing the active indices. I.e, the samples being considered in this step.

    Returns:
        best_feature (int):     The index of the best feature to split
    """    
    
    # Some useful variables
    num_features = X.shape[1]
    
    # You need to return the following variables correctly
    best_feature = -1
    max_information_gain = 0.
    
    for feature in range(num_features):
        information_gain = compute_information_gain(X, y, node_indices, feature)
        if information_gain > max_information_gain:
            best_feature = feature
            max_information_gain = information_gain
    ### END CODE HERE ##    
   
    return best_feature

核心递归函数建立决策树（先序遍历）：

# Not graded
tree = []

def build_tree_recursive(X, y, node_indices, branch_name, max_depth, current_depth):
    """
    Build a tree using the recursive algorithm that split the dataset into 2 subgroups at each node.
    This function just prints the tree.
    
    Args:
        X (ndarray):            Data matrix of shape(n_samples, n_features)
        y (array like):         list or ndarray with n_samples containing the target variable
        node_indices (ndarray): List containing the active indices. I.e, the samples being considered in this step.
        branch_name (string):   Name of the branch. ['Root', 'Left', 'Right']
        max_depth (int):        Max depth of the resulting tree. 
        current_depth (int):    Current depth. Parameter used during recursive call.
   
    """ 

    # Maximum depth reached - stop splitting
    if current_depth == max_depth:
        formatting = " "*current_depth + "-"*current_depth
        print(formatting, "%s leaf node with indices" % branch_name, node_indices)
        return
   
    # Otherwise, get best split and split the data
    # Get the best feature and threshold at this node
    best_feature = get_best_split(X, y, node_indices) 
    tree.append((current_depth, branch_name, best_feature, node_indices))
    
    formatting = "-"*current_depth
    print("%s Depth %d, %s: Split on feature: %d" % (formatting, current_depth, branch_name, best_feature))
    
    # Split the dataset at the best feature
    left_indices, right_indices = split_dataset(X, node_indices, best_feature)
    
    # continue splitting the left and the right child. Increment current depth
    build_tree_recursive(X, y, left_indices, "Left", max_depth, current_depth+1)
    build_tree_recursive(X, y, right_indices, "Right", max_depth, current_depth+1)

调用与运行结果展示：

build_tree_recursive(X_train, y_train, root_indices, "Root", max_depth=2, current_depth=0)

'''
 Depth 0, Root: Split on feature: 2
- Depth 1, Left: Split on feature: 0
  -- Left leaf node with indices [0, 1, 4, 7]
  -- Right leaf node with indices [5]
- Depth 1, Right: Split on feature: 1
  -- Left leaf node with indices [8]
  -- Right leaf node with indices [2, 3, 6, 9]
'''

Polaris6G's blog

机器学习-03

概念

关键点