激动人心的强化学习!
应用
- 机器人控制
- 工厂优化
- 金融股票交易
- 游戏AI
概念
奖惩机制
内部自己学习,黑盒
- State
- Action
- Reword
- new State’
the return 回报
折扣因子 discount factor
让算法关注眼前的程度(每一步长乘一个r,就像利率折现)

所以,该算法的效果可以总结为:
- 趁早得到正反馈
- 推迟遭受或不遭受负反馈
强化学习算法的目标:找到一个策略,在获知每一种所处情况下,可以提供相应的行动去最大化回报 State — function($\pi$) —> Action
马尔科夫决策过程 MDP
在强化学习中,智能体观测得到环境的当前状态之后,采取动作,环境进入下一个状态,智能体又得到下一个环境状态的信息,形成一个循环回路。
状态动作价值函数
Q函数

代码实现
贝尔曼方程

递归终点
random stochastic environment
模拟随机环境
会加入走相反方向或尝试其他操作的概率

最终未来回报部分演化为期望,即均值
连续状态空间应用
汽车控制(二维平面内假设):
- $x$ x轴位置
- $y$ y轴位置
- $\theta$ 面朝方向
- $\dot x$ x方向速度
- $\dot y$ y方向速度
- $\dot \theta$ 旋转角速度
直升机控制:
- $x$ x轴位置
- $y$ y轴位置
- $z$ 面朝方向
- $\phi$ 向左翻滚向右翻滚 x & z
- $\theta$ 向前翻滚向后翻滚 y & z
- $\omega$ 机头朝向 x & y
- $\dot x$ x方向速度
- $\dot y$ y方向速度
- $\dot z$ z方向速度
- $\dot \phi$ 向左翻滚向右翻滚 x & z
- $\dot \theta$ 向前翻滚向后翻滚 y & z
- $\dot \omega$ 机头朝向 x & y
实际案例:登月器

状态定义:
- $x$ x轴位置
- $y$ y轴位置
- $\dot x$ x轴径向速度
- $\dot y$ y轴径向速度
- $\theta$ 偏离角度
- $\dot \theta$ 角速度
- $l$ 左脚是否着地(二进制 01)
- $r$ 右脚是否着地(二进制 01)
奖惩函数:
- 降落到指定区域:100~140(根据降落位置差别给出)
- 对于靠近着陆点奖励,对于远离着陆点惩罚
- Crash:-100
- 软着陆:+100
- 有腿着陆:+10
- 每启动一次主推进器(向上推进):-0.3
- 每启动一次侧推进器(向左右推进):-0.03
深度强化学习
DQN
输入向量:
- 8个状态特征 + 4个行为特征(nothing,left,main,right)
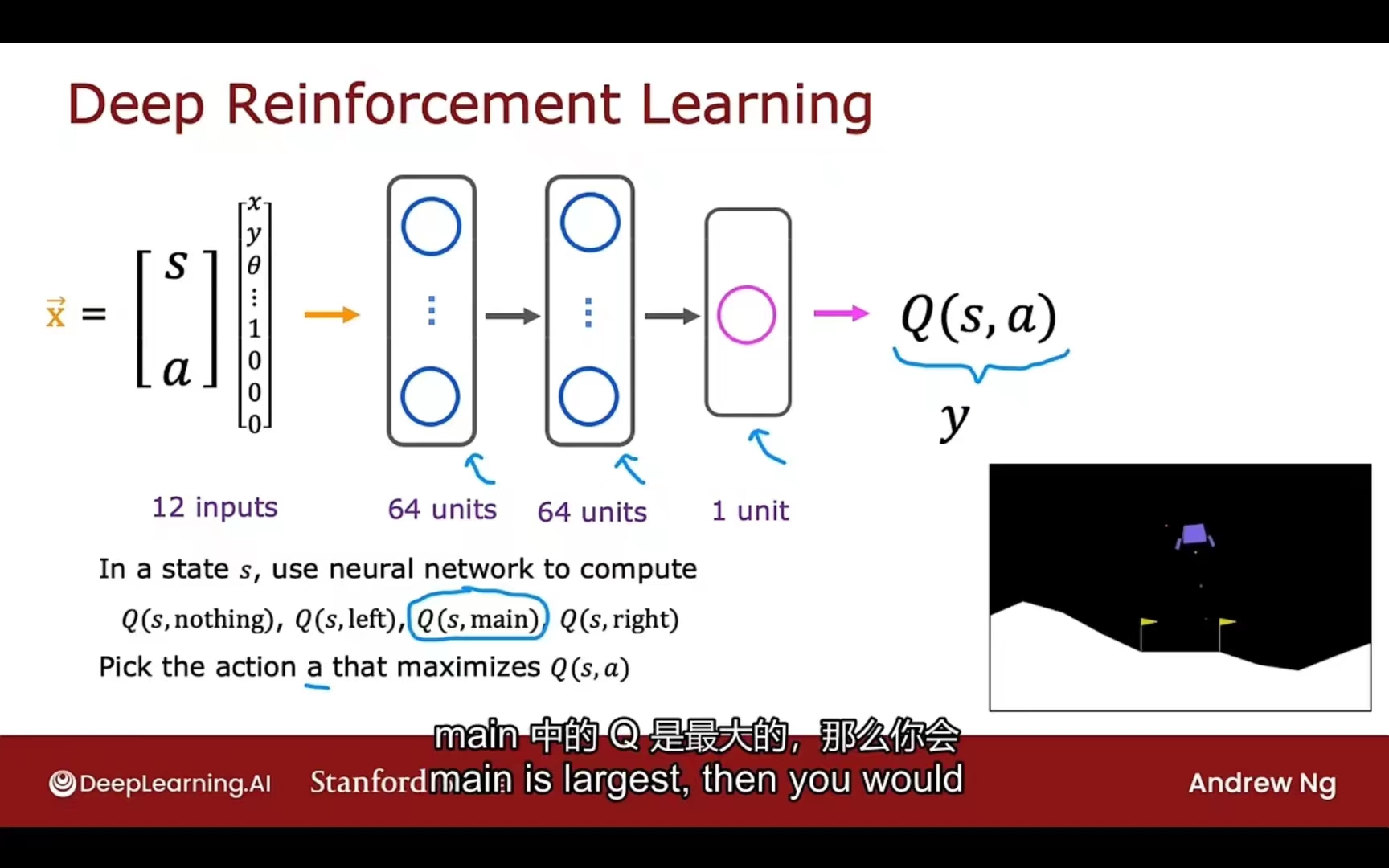
- 迭代地创建映射数据和训练网络,优化模型

改进方式
输出改进
输出从一个特征转为四个特征,之后选最大值即可
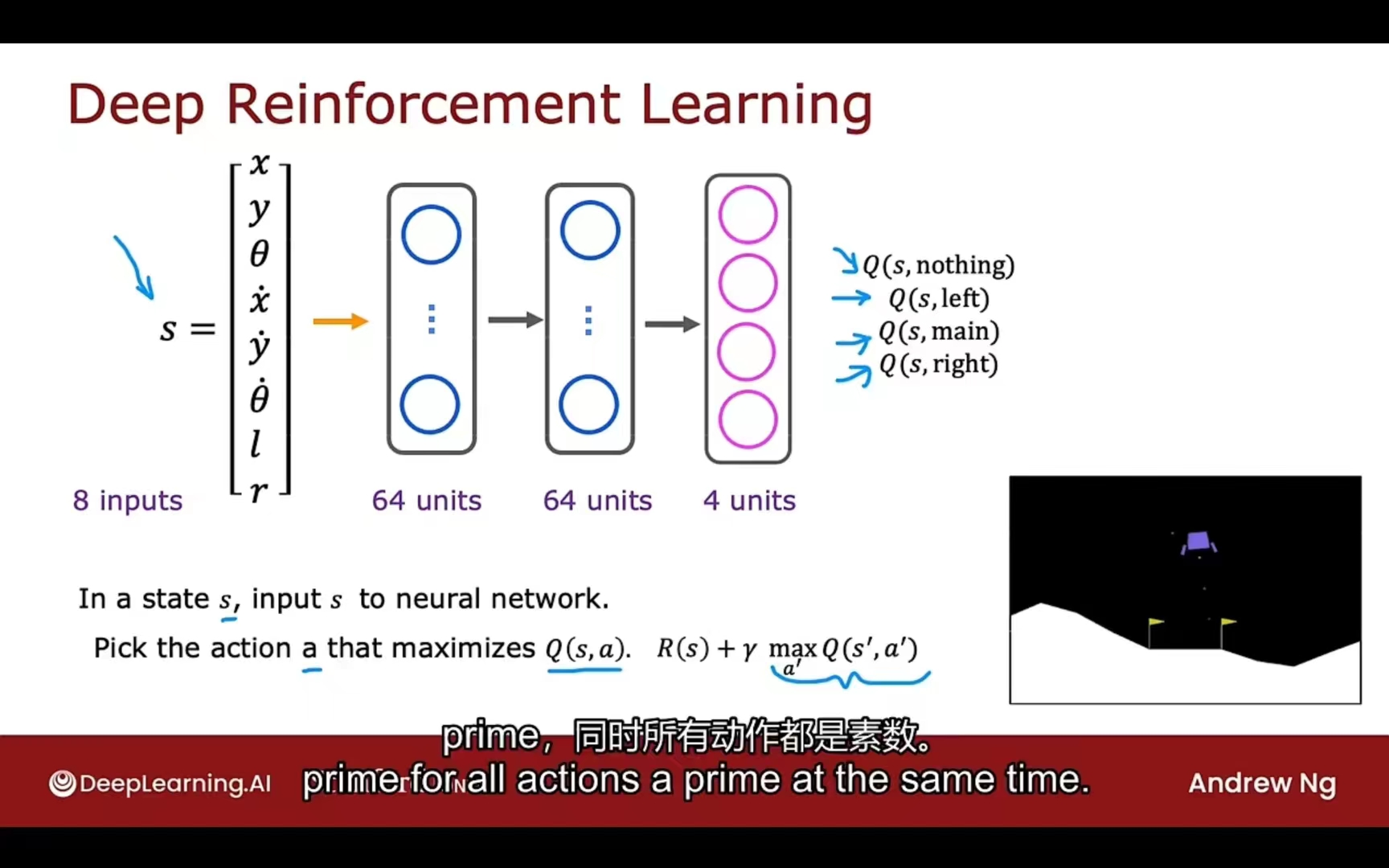
$\epsilon$贪婪策略
随机选取 -> 有目的选取
方式一:
选取行动a使得最大化$Q(s, a)$
方式二:
95%概率选取行动a最大化$Q(s, a)$;(剥削步骤 Exploitation)
5%概率随机选取行动a (探索步骤 Exploration)
其中$\epsilon$ = 0.05
$\epsilon$的变化过程:Gradually decrease(1.0 -> 0.01)
注意:超参数的选择很重要,选择不好训练会花费的时间可能超级加倍
小批量
mini-batch
如果数据量太大,每一次计算损失函数和梯度下降的过程都要全部过一遍,速度会极慢
可以选择每次迭代都换一批训练集,使用不同的小的训练集进行迭代训练和梯度下降,效果会如下:
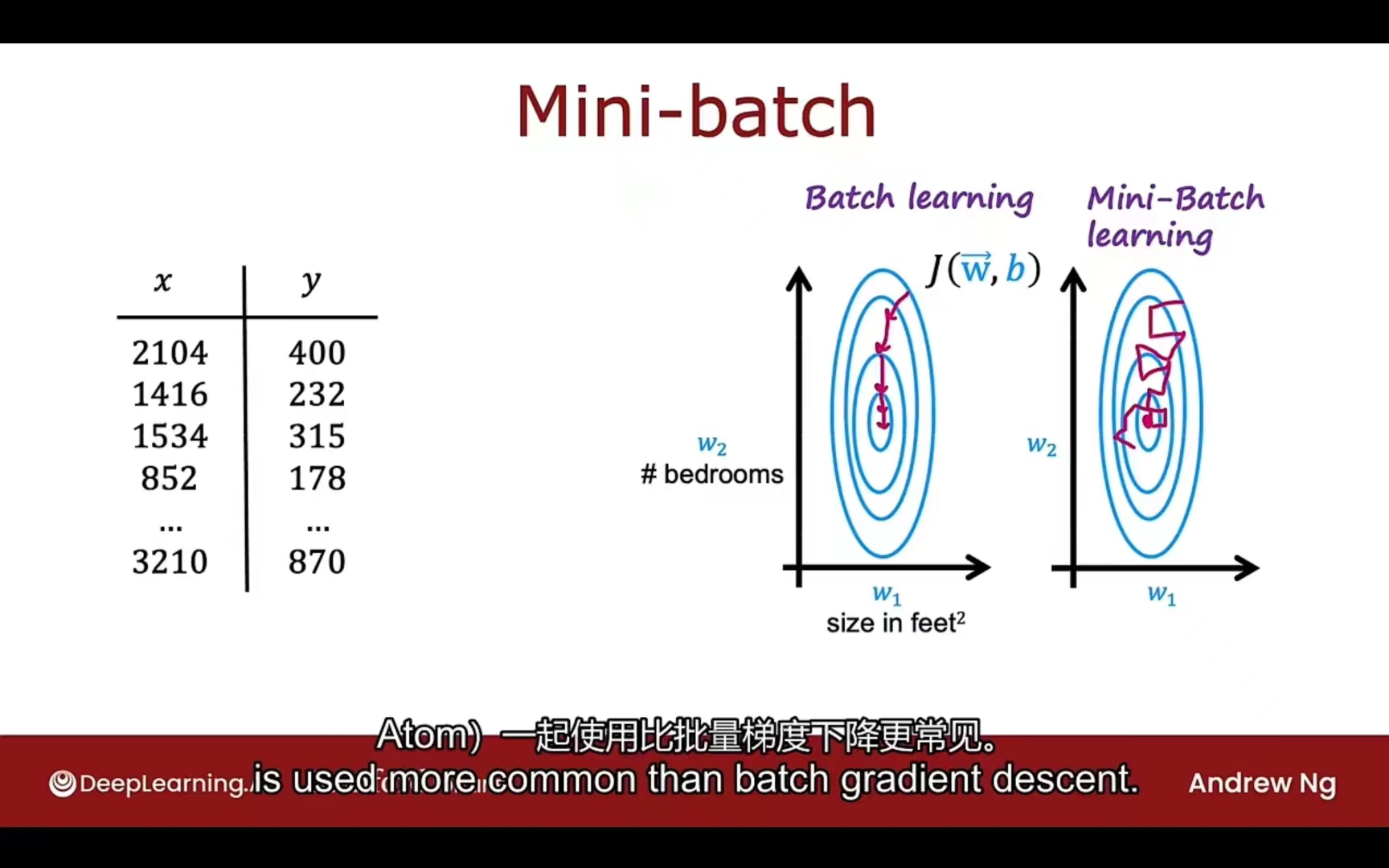
对应到应用的改进:

软更新
$Set Q = Q_{new}$转变为:
$W = 0.01 W_{new} + 0.09W$
$B = 0.01B_{new} + 0.99B$
强化学习的局限性
- 将强化学习运用到模拟环境或游戏中的难度会比真正运用到机器人的难度要低,所以要找好技术适用方向
- 如今的强化学习运用远比监督和无监督学习少
- 强化学习的未来研究潜力会很大
总结
